Grado 10 - Trigonometría - Angulos, longitud de arco, velocidad angular y lineal, triángulos, teorema de pitágoras.

ANGULOS
Un Angulo AOB está formado por dos semi rectas R1, R2 con un vértice común O, con frecuencia interpretamos un ángulo como una rotación de la semi recta R1 sobre R2. en este caso R1 recibe el nombre de lado inicial y R2 es el lado terminal del ángulo. si la rotación es en el sentido contrario a las manecillas del reloj, el ángulo es considerado positivo y si es en sentido de las manecillas del reloj el ángulo es negativo.
La medida de un ángulo es la cantidad de rotación alrededor del vértice para mover R1 sobre R2. esto es: cuánto es lo que abre el ángulo en palabras cotidianas. Una unidad de medida para ángulos muy utilizada son los grados. Un ángulo de medida 1 grado se forma el girar el lado inicial 1/360 de una revolución (vuelta) completa.
1. Ángulos en posición normal
Un ángulo trigonométrico está en Posición Normal si su vértice está en el origen de coordenadas y su lado inicial coincide con el lado positivo del eje X y el otro está en cualquier cuadrante

Si el
lado final coincide con un eje se dice que el ángulo no pertenece a ningún
cuadrante. Ej:

Nota: Cuando el ángulo no está en posición normal se le conoce como ángulo cuadrantal
2. Ángulo Cuadrantal

Un ángulo en posición normal se llamará Cuadrantal cuando su lado final coincide con un eje. En consecuencia, no pertenece a ningún cuadrante.
Los principales ángulos cuadrantes son: 0º, 90º, 180º, 270º y 360º, que por "comodidad gráfica" se escribirán en los extremos de los ejes.
Signos de la razón trigonométrica en cada cuadrante:
Para hallar los signos en cada cuadrante existe una regla muy práctica
Son Positivos:

Nota: Pídele al docente una calculadora para que compruebas las razones trigonométricas en cada cuadrante y llena la siguiente tabla:

Si quieres observar el cuadro ya realizado para que lo compares con el tuyo; con tu celular escanea el siguiente código QR:

PRÁCTICA.
Practica lo visto de ángulos positivos y negativos en el siguiente enlace:
VIDEO:
Para afianzar el tema observa el siguiente video:
3. Razones trigonométricas de ángulos en posición normal
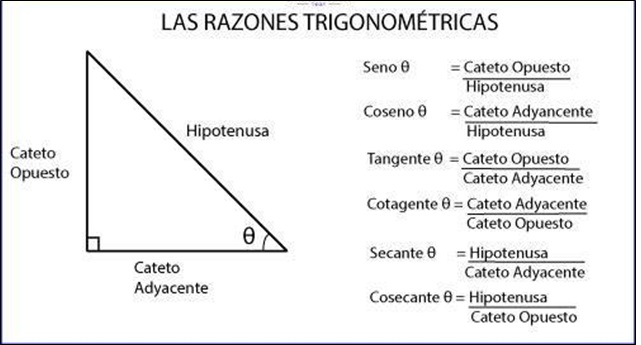
Si 𝜃 es un ángulo cualquiera en posición normal, sus razones trigonométricas se definen como sigue:

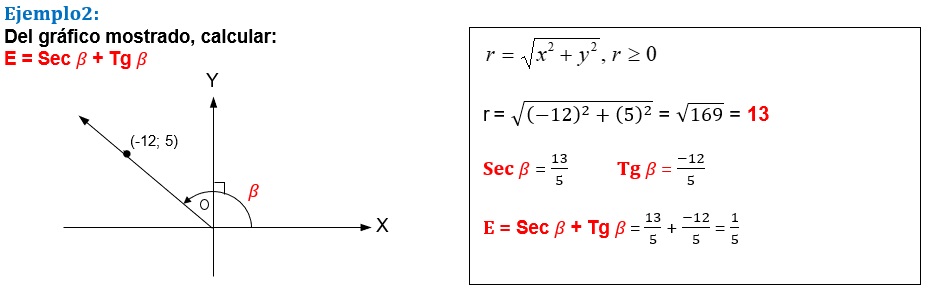
Para realizar los siguientes ejemplos, les recuerdo las razones trigonométricas ya vistas de acuerdo a Pitágoras:


VIDEO:
Para afianzar el tema sobre razones trigonométricas de un ángulo en posición normal observa el siguiente video:






4. Sistemas de medidas de ángulos:
Las unidades utilizadas con mayor frecuencia para medir los ángulos son el grado sexagesimal y el radián.
4.1. Sistema Sexagesimal: El Sistema sexagesimal mide el tiempo y los ángulos.
Es un sistema de numeración de base 60, es decir, cada unidad se divide en 60 unidades de orden inferior.
1 grado (1°) = 60 minutos (60'), también 1 hora = 60 minutos.
1 minuto (1') = 60 segundos (60").

Ejemplo:
Convertir 32. 72°
1. Para convertir grado decimal a grado, minutos y segundos, las unidades enteras de los grados se quedarán como están. Multiplica los decimales por 60. El número entero se convierte en los minutos.
0,72 x 60 = 43,2
32° 43'
2. Tomo el decimal restante y lo sigo multiplicando por 60 y tomo el resultado entero para los segundos.
0,2 x 60 = 12
Respuesta: 32° 43' 12"
5. Operaciones en el sistema sexagesimal:
5.1. Suma:
1. Se ubican en columnas, es decir van sumando cada una de las columnas empezando por los segundos.
2. Se van sumando cada una de las columnas empezando por los segundos.
3. Si los segundos sumados superan los 60'', se les resta 60'' y se suma 1' en la siguiente columna a la izquierda.
4. Si los minutos sumados superan los 60', se les resta 60' y se suma 1º en la siguiente columna a la izquierda.
Ejemplo:
Sumar las siguientes coordenadas en sexagesimal

5.2. Resta:
1. Se ubican en columnas, una debajo de otra (segundos con segundos, minutos con minutos y grados con grados)
2. Se van restando cada una de las columnas empezando por los segundos.
3. Si los segundos restados son un número negativo, se suma 60'' y se resta 1' en la siguiente columna a la izquierda.
4. Si los minutos restados son un número negativo, se suma 60' y se resta 1º en la siguiente columna a la izquierda.
Ejemplo:
Restar las siguientes coordenadas en sexagesimal

VIDEO:
Si no te quedó claro el tema de operaciones de ángulos en el sistema sexadecimal, te invitamos a observar el siguiente video:
ACTIVIDAD2.
1. Realizar en el cuaderno los siguientes ejercicios de suma de ángulos:
2. Realizar en el cuaderno los siguientes ejercicios de resta de ángulos:
6. Relación entre grados y radianes:
Pero en cálculo y en otras ramas de la matemática se usa otro método de medir ángulos y es la medida en radianes (rad), la cantidad que abre un ángulo se mide a lo largo del arco de una circunferencia de lado 1 con su centro en el vértice del ángulo.
La circunferencia del círculo de radio 1 es 2π y, por lo tanto, una revolución completa tiene medida 2π rad. Recordemos que un ángulo llano tiene una medida de π rad y un ángulo recto tiene una medida de 2/π rad.

Medidas en Radianes (rad). Una revolución completa
es 360°, que es lo mismo que 2π en radianes.

Ejemplos:
1. Convertir los siguientes grados a radianes

Si no te quedó claro el tema de conversión de grados a radianes y viceversa, te invito a observar el siguiente video:
ACTIVIDAD3:
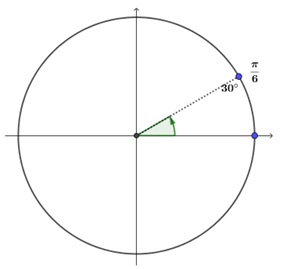
a) Expresa en grados y radianes todos los ángulos entre 0 y 180 que sean múltiplo de 30. Debes expresarlos en la siguiente circunferencia.
b) Expresa en grados y radianes todos los ángulos entre 180 y 360 que sean múltiplo de 45. Debes expresarlos en la siguiente circunferencia.

7. Ángulos Coterminales
Son aquellos ángulos en posición normal que con diferente medida coinciden en su lado inicial y su lado final, en la gráfica anterior los ángulos (a) y (c) son coterminales.


Ejemplo1:
Encuentre ángulos que sean coterminales con el ángulo 𝜃=30° en posición normal.
Solución:
Para hallar ángulos positivos que sean coterminales con 𝜃, sumamos cualquier múltiplo de 360°, así:
30° + 360° = 390° y 30° + 720 = 750°
Son coterminales con 𝜃=30° por el lado negativo restamos cualquier múltiplo de 360° así:
30° - 360° = -330° y 30° - 720 = -690°

VIDEO:
Observa el siguiente video sobre ángulos coterminales para reforzar el tema:
Acá te dejo la relación de ángulos en grados y su respectivo en radianes:

ACTIVIDAD4




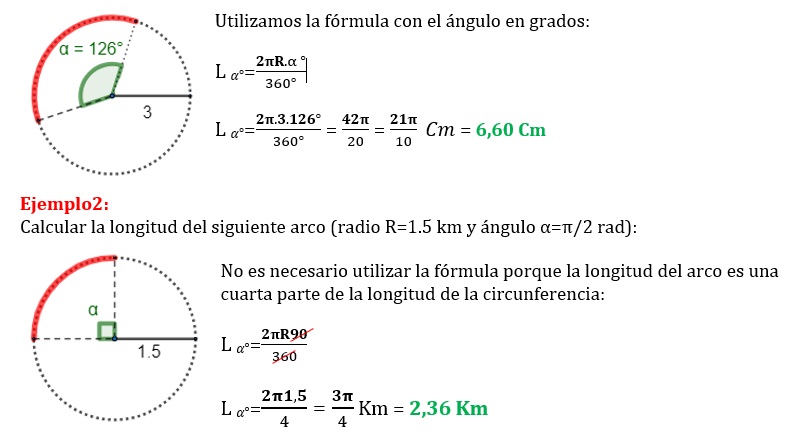




VIDEO
Sino te quedó claro el tema sobre longitud de arcos, te invito a observar el siguiente video:
Actividad5
Desarrolla los ejercicios del link, cópialos en el cuaderno y cuando termines muéstrale los resultados al docente.
9. AREA DE SECTOR CIRCULAR
¿Qué es un círculo?
Es el conjunto de puntos en el plano que se encuentran contenidos en el interior y sobre una circunferencia.
¿Qué es un sector circular?

Metiendo esta ecuación en la fórmula inicial obtenemos otras formas de poder expresar el área de un sector circular.
Fórmulas para hallar el área del sector circular
Entonces la fórmula para calcular el sector circular sería:





Actividad 6:
1. Halla el área del sector circular:







Videos
Sino te quedó claro el tema de velocidad angular y lineal, observa los siguientes videos:
Actividad 7:
1. Pasar de revoluciones por minuto a radianes/s
a) 20 r.p.m
b) 50 r.p.m
c)120 r.p.m
2. ¿Cuál es la velocidad, en rad/s, de una rueda que gira a 300 r.p.m.? Si el diámetro de la rueda es de 90 cm calcular la velocidad lineal en un punto de su periferia ¿
3. Siendo 30 cm el radio de las ruedas de un coche y 900 las revoluciones que dan por minuto, calcule:
a) la velocidad angular de las mismas;
b) la velocidad del coche en m/s y en km/h;
4. Un coche circula a una velocidad de 90 Km/h, si el radio de las ruedas del coche es de 30 cm calcular
a) su velocidad lineal en m/s .
b) la velocidad angular de las ruedas en rad /s y r.p.m
5. La rueda de una bicicleta tiene 30 cm de radio y gira uniformemente a razón de 25 vueltas por minuto. Calcula:
a) La velocidad angular, en rad/s.
b) La velocidad lineal de un punto de la periferia de la rueda.
c) Angulo girado por la rueda en 30 segundos
d) número de vueltas en ese tiempo
6. Un satélite describe un movimiento circular uniforme alrededor de la Tierra. Si su velocidad angular es de 0,5 vueltas por hora, calcula el número de vueltas que da en un día.
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%): a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%): a. Prueba Bimestral
• Ser - Convivir (25%): a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
1. Nunca (1.0) 2. Casi Nunca (2.0) 3. A veces (3.0) 4.Casi Siempre (4.0) 5. Siempre (5.0)
AUTOEVALUACION COMPONENTE HACER Y SER - CONVIVIR
(La realiza el estudiante)

TALLER DE NIVELACION Y REFUERZO: Se aplicará en la durante el periodo de acuerdo a las actividades asignadas por el docente
