Grado 11 P3 - Cálculo - Límites y funciones

1. CONCEPTOS
El concepto de límite en matemáticas tiene el sentido de "lugar" hacia el que se dirige una función en un determinado punto o en el infinito (En Y). Dada una función f(x) y un punto x=a se dice que el límite de f(x) cuando x se acerca a a es L, y se expresa como:

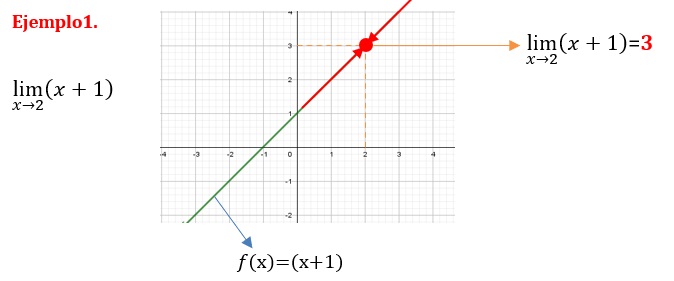
Cuando el límite tanto por la izquierda como por la derecha se acerque a 2 la función f(x) o y va a ser igual a 3.

Ojo. Cuando un límite se acerca por un lado a un número y por el otro a otro número (2 números) ese límite no existe. Tienen que acercarse todas las líneas al mismo punto. En el ejemplo de la derecha se acerca a 1 pero por el otro lado no se acerca a nada porque no hay continuidad

Usos de las funciones con límites:
Las funciones matemáticas se utilizan en otros ámbitos, por ejemplo, para calcular los beneficios o los costes de una empresa, la velocidad o aceleración de un móvil, etc., por lo que es importante conocer el comportamiento de una función.
Por ejemplo, la siguiente función no está definida en x=0 ni en x=-1 (Por que no se puede dividir entre 0)

Sin embargo, sí podemos preguntarnos cómo se comporta la función cuando x se aproxima a 0 o cuando se aproxima a −1. ¿Y si x crece o decrece indefinidamente? Los límites de la función f nos proporcionan las respuestas.
Además de ayudarnos a visualizar la gráfica de la función, los límites también se utilizan para estudiar otras propiedades, como la continuidad de una función, la diferenciabilidad, etc.
2. LÍMITES EN UN PUNTO
El límite de una función f(x) en el punto a, es el valor que se obtiene cuando sustituimos el valor de x=a en la función:

Nota: Pero no siempre calcular el límite es tan fácil, hay algunas funciones que al sustituir no nos da un valor en concreto y tenemos que realizar una serie de cálculos para poder obtener el valor. Estos casos especiales son los conocemos como indeterminaciones.
Ejemplo2:


No existe f(0), pero cuanto más se aproxima x a 0, la función crece más y más, como podemos observar en la gráfica:
Por tanto, el límite de f cuando x tiende a 0 es infinito:

También, podemos predecir el comportamiento de la función cuando x crece o decrece indefinidamente (cuando x tiende a ±∞). Cuando esto ocurre, la función f(x)=1/x2 se aproxima cada vez más a 0.

VIDEO:
Si no entendiste el tema, te invito a reforzar a través del siguiente video:
2. Desarrollar los siguientes ejercicios en el cuaderno:
https://es.liveworksheets.com/worksheets/es/Matem%C3%A1ticas/L%C3%ADmites/L%C3%ADmites_sx1200383bc
PROPIEDADES DEL LÍMITE DE UNA FUNCIÓN EN UN PUNTO
Dadas f(x) y g(x) dos funciones, se cumple:
A. El límite de una suma o resta es igual a la suma o resta de los límites.

B. El límite de un cociente es igual al cociente de los límites.

C. El límite de un producto es igual al producto de los límites.

D. El límite de una potencia:

E. Una de las propiedades más importantes es la que utilizamos para resolver indeterminaciones con potencias:

2. INDETERMINACIONES
Como ya hemos comentado en la nota del primer apartado, cuando resolvemos un límite aplicando las propiedades nos podemos encontrar con situaciones especiales: las indeterminaciones. Nos encontramos 3 tipos distintos:
Tipo 1: Indeterminación 0/0.
En este tipo de indeterminación nos podemos encontrar dos casos distintos:
Caso a. Que resolveremos factorizando, ya sea por Ruffini o sacando factor común. Una vez que simplificamos, volvemos a sustituir por el valor de x:

Caso b. Cuando en la función hay raíces cuadradas, tenemos que multiplicar numerador y denominador por el conjugado. Operamos teniendo en cuenta que suma por diferencia es diferencia de cuadrados, desapareciendo la raíz en el numerador o denominador. A continuación, si volvemos a obtener la indeterminación 0/0, volvemos al caso a) y tenemos que factorizar y simplificar:

Tipo 2: Indeterminación k/0.
Aunque este tipo no es exactamente una indeterminación, pero se considera un caso especial, ya que, aunque siempre que tenemos k/0=∞, tenemos que realizar los límites laterales para determinar el signo del infinito. Este tipo de límites es el que nos aparece siempre que estudiamos las asíntotas verticales.

Tipo 3: Indeterminación 1 elevado a ∞.
Teniendo en cuenta la propiedad número 5, este límite se puede resolver haciendo transformaciones para llegar a una expresión similar, o utilizando la siguiente fórmula:

Vamos a resolver el siguiente ejemplo utilizando únicamente la fórmula:

VIDEO:
Sino te quedo claro el tema de indeterminaciones en límites, te invito a ver el siguiente video:
Actividad2:
1. Halle los siguientes límites:












VIDEOS:
Te invito a observar los siguientes videos sobre límites trigonométricos:
Actividad 4:
Desarrolla los siguientes límites en el cuaderno:



Por último, es necesario que el valor de la imagen sea igual que el valor del límite
Por tanto, una función puede dejar de ser continua en un punto por no cumplir alguna de estas tres condiciones. En este caso (si no se cumple alguna de las condiciones) diremos que la función es discontinua en dicho punto. En caso de que no se cumpla la segunda condición, la función no estaría definida en el punto x = a y no podríamos hablar ni de continuidad ni discontinuidad en dicho punto.
Ejemplo de los tres casos:


a. Imagen en x = 2
f(2) = 2.5
Por lo tanto, la función sí tiene imagen en el punto x = 2
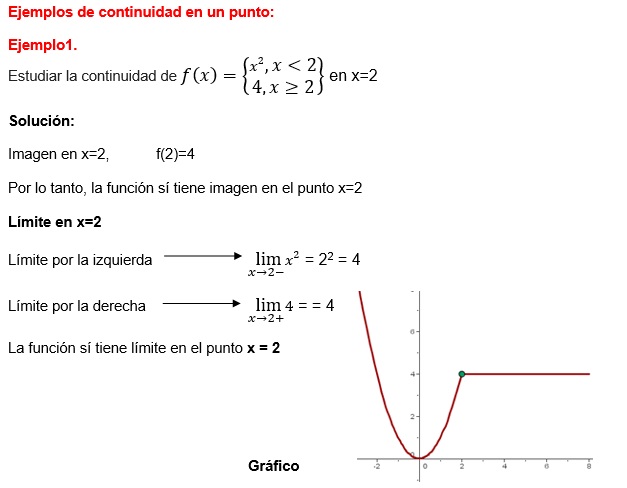
b. Límite en x = 2


VIDEO:
Te invito a observar el siguiente ejemplo de continuidad en un punto:





VIDEOS:
Si quieres aprender más sobre el tema de funciones continuas, te invito a que observes el siguiente video:
https://www.youtube.com/watch?v=d2AN1MzQfYg
Actividad 5
1. Ir al enlace y realizar los ejercicios en esta página, cuando terminas enséñale los resultados al docente para que te pregunte y evalúe.
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%): a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%): a. Prueba Bimestral
• Ser - Convivir (25%): a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
1. Nunca (1.0) 2. Casi Nunca (2.0) 3. A veces (3.0) 4.Casi Siempre (4.0) 5. Siempre (5.0)
AUTOEVALUACION COMPONENTE HACER Y SER - CONVIVIR
(La realiza el estudiante)
