Grado 6 P3 - Estadística - Medidas de tendencia central

Corresponden a valores que generalmente se ubican en la parte central de un conjunto de datos.
Las medidas estadísticas pretenden "resumir" la información de la "muestra" para poder tener así un mejor conocimiento de la población. Son valores representativos de la totalidad de los datos. Su cálculo permite analizar los datos en torno a un valor central. Los valores centrales más usados son:
1. Media aritmética (Promedio) - X
Es la suma de un conjunto de valores dividida por el número total de ellos. Para hallar la media en un conjunto de datos, basta con sumar todos los datos y dividirlos entre el número total de datos.
La media aritmética es el mismo concepto que conocemos como «promedio».
Ejemplos
1. Hallar la media aritmética de los siguientes datos 14; 16; 12; 12; 10; 18; 20; 14
Lo primero que hay que hacer es sumar todos los valores que nos dieron, luego se divide entre el número total de datos, en este caso, son 8 datos. Por lo tanto, la media o promedio de esos datos es 14,5.

2. Dada la tabla de distribución de frecuencias, calcular la media aritmética.

En este caso, debo tener en cuenta que como tengo la tabla de frecuencia, los datos están organizados, lo que significa que debo estar atento y reconocer cuantos estudiantes sacaron la misma nota. Por lo tanto,

La media o promedio es 12,45.
ACTIVIDAD1
1. Se Obtuvo los datos de consumo de café del 2005 al 2014, la empresa Santafé Coffe S.A.S desea conocer el promedio o media aritmética de:

A. consumo por año
B. Consumo por ciudad
C. Por edad
2. Mediana (Me)
Es el valor de la variable que deja igual número de datos antes y después de él en una distribución de frecuencia. Si la distribución tiene número impar de datos, la mediana será el valor que quede en el centro, después de ordenar todos los valores de menor a mayor. Si la distribución tiene número par de datos, la mediana se calcula sumando los dos valores que quedan en el medio y dividiendo entre dos.
Ejemplos
1. Halla la mediana de los siguientes datos 6, 10, 7, 8, 13, 11, 9, 12, 14.
Lo primero que hacemos es contar el número de datos, en este caso, son nueve, lo que significa que por ser 9 un número impar, la mediana queda en el centro de la distribución. Luego organizamos los datos de menor a mayor:
6, 7, 8, 9, 10, 11,
12, 13, 14
Se puede observar que 10 es el número que queda en el centro de los demás, antes quedan cuatro números y después quedan cuatro números, por tanto, 10 es la mediana.
2. Encuentre la mediana del conjunto 3, 10, 36, 255, 79, 24, 5, 8
Organizamos los datos de menor a mayor, nos damos cuenta que son 8 datos, por tanto, debo sumar los dos valores que queden en el medio y dividir entre dos.
3, 5, 8, 10, 24, 36,
79, 255
Los datos que quedan en la mitad son 10 y 24, por tanto, se suman:

17 es la mediana.
3. Moda (Mo)
Es el valor de la variable que tiene mayor frecuencia absoluta, en otras palabras, es el dato que más de repite.
Ejemplos
1. Halla la moda de los siguientes datos 7; 8; 9; 10; 11; 10; 7; 7
Como la moda es el dato que más se repite, basta con identificar cuál es el valor o el dato que se repite mayor cantidad de veces.
En este caso la moda es 7 porque se repite más veces que los demás datos.
2.
Halla la moda en la siguiente distribución

La variable que tiene mayor frecuencia es 160, por tanto, esa la moda.
Ejemplo general
El profesor Andrés reunió los puntajes de las pruebas de sus estudiantes y obtuvo los siguientes datos:
90, 76, 53, 78, 88, 80, 81, 91, 99, 68, 62, 78, 67, 82, 88, 89, 78, 72, 77, 96, 93, 88, 88.
Encuentra la media, la mediana y la moda de estos datos.
Media
53 + 62 + 67 + 68 + 72 + 76 + 77 + 78 + 78 + 78 + 80 + 81 + 82 + 88 + 88 + 88 + 88 + 89 + 90 + 91 + 93 + 96 + 99 = 1.862

La media o promedio es 80,95
Mediana
53, 62, 67, 68, 72, 76, 77, 78, 78, 78, 80, 81, 82, 88, 88, 88, 88, 89, 90, 91, 93, 96, 99 El dato que queda en el centro es 81, por tanto, es la mediana.
Moda
La moda es el dato que más se repite, por tanto, es 88.
Si te ha quedado alguna duda puedes observar el siguiente video:
https://www.youtube.com/watch?v=0DA7Wtz1ddg
ACTIVIDADES
Resuelve los
siguientes ejercicios:
1. Hallar la media aritmética, la mediana y la moda de los siguientes datos, si desean puedes diseñar una tabla.
a. 10, 12, 10, 11, 11, 13, 14, 15, 16
b. 4, 6, 7, 8, 5, 6, 6, 3, 4, 7, 3, 9, 8, 8, 6, 5, 4, 3, 4, 7, 8, 7, 8, 6, 9, 4, 3, 5, 5, 6, 6, 5, 6, 7, 8, 4, 3, 4, 6, 9, 6, 5, 7, 6, 8, 7, 3, 4, 9, 9.
c. 6, 6, 5, 2, 3, 4, 4, 5, 5.
2. Durante el mes de mayo, en Copacabana, se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.
Hallar la media, la mediana y la moda.
3. Hallar la media, la mediana y la moda de las
siguientes tablas
Experimento aleatorio, espacio muestral, evento y probabilidad
Veamos ahora la definición clásica de probabilidad, además de las definiciones de experimento, espacio muestral y evento.

Experimento aleatorio
Es la reproducción controlada de un fenómeno; y cuyo resultado depende del azar. Ejemplos:
- Lanzamiento de un dado.
- Lanzamiento de una moneda.
Un experimento aleatorio puede ser repetido bajo las mismas condiciones, y se puede describir el número de resultados posibles.
Espacio muestral (S)
Es el conjunto de todos los resultados posibles de un experimento aleatorio.
- Si se lanza un dado, el espacio muestral está compuesto por los siguientes elementos: S={1, 2, 3, 4, 5, 6}.
- Si se lanza una moneda que tiene dos caras: perro (P) y gato (G), el espacio muestral está compuesto por: S={P, G}.
- Si se lanzan dos monedas, el espacio muestral está compuesto por: S={(P, P), (P, G), (G, P), (G, G)}.
- Si se lanza un dado y una moneda, el espacio muestral está compuesto por: S={(1,P),(1,G),(2,P),(2,G),(3,P),(3,G),(4,P),(4,G),(5,P),(5,G),(6,P),(6,G)}
Actividad1:
1. En una bolsa hay 10 bolas numeradas del 11 al 20, algunas rojas otras verdes y otras azules.

Sacamos sin mirar una bola,
- ¿cuál es el espacio muestreal numérico?
- ¿cuál es el espacio muestreal de colores?
Evento o suceso
Conjunto de uno o más resultados del experimento aleatorio.
- Si A = {obtener un número 5 al lanzar un dado}, entonces, A={5}.
- Si B = {obtener un número mayor que 3 al lanzar un dado}, entonces, B={4, 5, 6}.
- Si C = {obtener un número par al lanzar un dado}, entonces, C={2, 4, 6}.
- Si D = {obtener al menos 1 gato al lanzar 2 monedas}, entonces, D={(P, G), (G, P), (G, G)}
Probabilidad
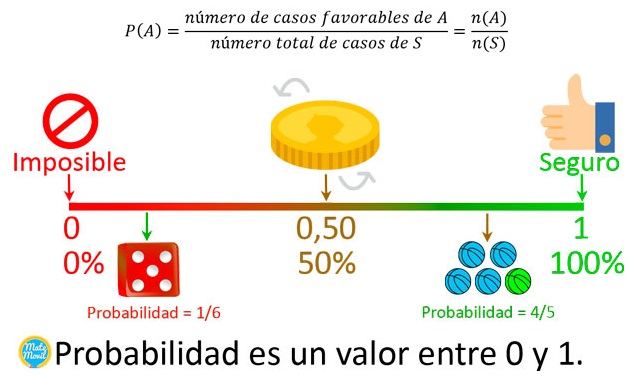
Probabilidad es un valor entre 0 y 1, que indica la posibilidad relativa de que ocurra un evento. El valor de la probabilidad se calcula mediante la siguiente fórmula:
Recuerda que...
- El valor de la probabilidad siempre se encuentra entre 0 y 1 (incluidos ambos números), es decir, 0 ≤ P(A) ≤1.
- La probabilidad de que ocurra un evento imposible es 0. Por ejemplo, la probabilidad de obtener un 8 al lanzar un dado numerado del 1 al 6 es 0, es decir, P(X)=0.
- La probabilidad de que ocurra un evento seguro es 1. Por ejemplo, la probabilidad de obtener un número menor que 7 al lanzar un dado numerado del 1 al 6 es 1, es decir, P(X)=1.
Ejemplo 1:
Calcular la probabilidad de obtener un 2 al lanzar un dado.
Solución:
Vamos a utilizar la fórmula de probabilidad:
El experimento consiste en lanzar un dado. Luego, definimos los resultados o casos del espacio muestral.
S = {1, 2, 3, 4, 5, 6}
Definimos nuestro evento A, como obtener un 2 al lanzar un dado. Ahora, calculamos el número de casos favorables del evento A.
A = { 2 }
Ahora, empleamos la fórmula:

El experimento consiste en lanzar un dado. Luego, definimos los resultados o casos del espacio muestral.
S = {1, 2, 3, 4, 5, 6}
Definimos nuestro evento A, como obtener un 2 al lanzar un dado. Ahora, calculamos el número de casos favorables del evento A.
A = { 2 }
Ahora, empleamos la fórmula:

Guía de ejercicios
En la siguiente guía encontrarás muchísimos problemas de probabilidades resueltos, el cual debes responder el planteamiento (División) de los ejercicios del 1 al 12
En el siguiente video, vamos a revisar la definición de experimento aleatorio, espacio muestral, evento
y probabilidad
