Grado 6 P3 - Geometría - Plano Cartesiano
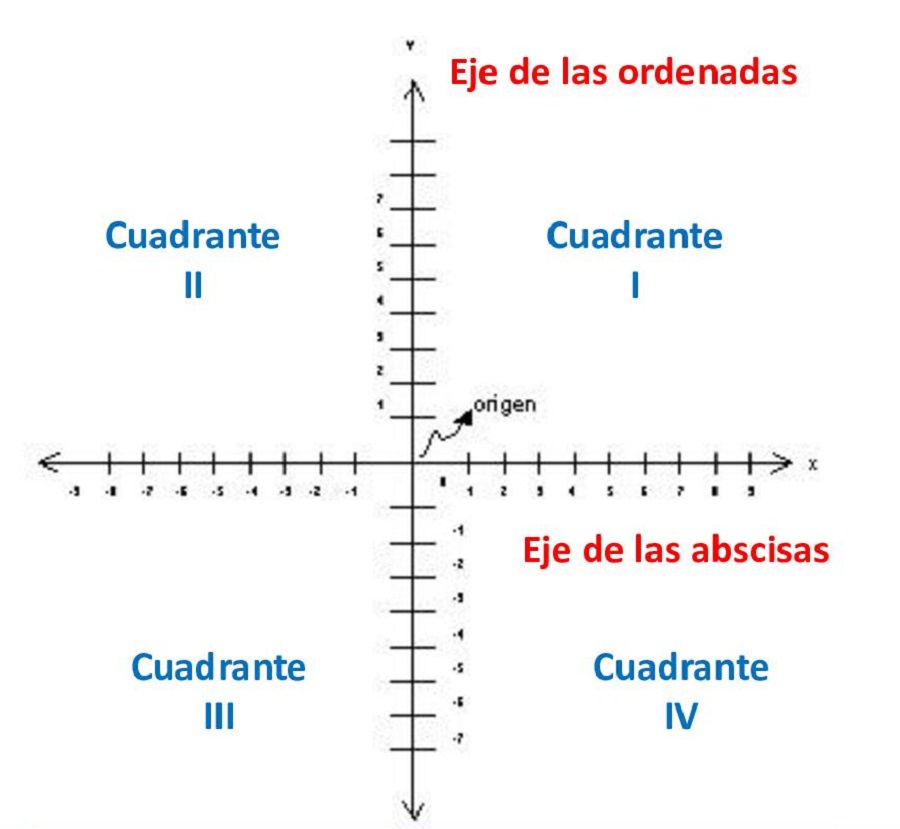
Recordemos: El plano cartesiano es como un mapa formado por dos rectas numéricas llamadas ejes. Estos ejes se intersecan o se cruzan formando un ángulo recto (90 grados).
Los ejes son: eje de las x y el eje de las y. Los ejes dividen el plano en cuarto partes llamadas cuadrantes.
Cada punto en el plano cartesiano puede representarse con un par ordenado de números (x, y).
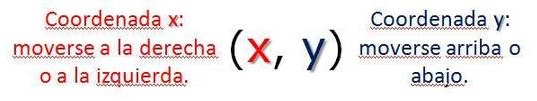
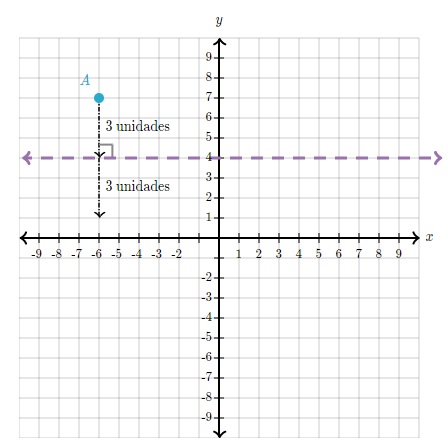
Para trazar un punto de un par ordenado, parte del origen, el punto (0, 0), donde se cruza el eje de las x y el eje de las y. La primera coordenada indica las unidades que hay que desplazarse en x, a la izquierda o a la derecha; la segunda indica cuántas unidades hay que subir o bajar. Ejemplo1:
Ejemplo2:
Ejemplo3:
PRACTICANDO
Haz clic en el enlace abajo para jugar en el plano cartesiano (Completar mínimo 5000 puntos)
https://wordwall.net/es/resource/12195194/plano-cartesiano
Haz clic en el enlace abajo para ver el video sobre trazar puntos en el plano cartesiano:
https://www.youtube.com/watch?v=v1_fJoy8oZU
Baja el archivo de Excel y explora trazando puntos en el plano cartesiano:
Haz clic en el enlace abajo para acceder a una prueba de práctica sobre marcar puntos en el plano cartesiano.
Haz clic en el enlace abajo para acceder a una prueba de práctica sobre identificar puntos en el plano cartesiano. Tendrás que escribir las coordenadas.
2. Transformaciones Isométricas en el plano cartesiano
Una transformación Isométrica es un movimiento que se realiza a una figura plana, de manera que esta mantiene, su forma y tamaño. A la figura resultante de la transformación Isométrica se le denomina figura imagen.
Las isometrías pueden ser consideradas como acciones o movimientos
que permiten copiar figuras sin perder su forma y tamaño. También se les
llama por esto "movimientos rígidos".
Entre las transformaciones isométricas que estudiaremos se encuentran las traslaciones, las rotaciones y las reflexiones o simetrías. Cuando trabajemos con cualquiera de estas tres transformaciones nos sería útil acudir a un sistema de coordenadas para poder describir la posición de diferentes puntos que forman nuestras figuras a transformar.
A. Traslación
Una traslación corresponde a un movimiento de una figura en una dirección fija, por lo tanto lo que se realiza es un desplazamiento que produce un cambio en la posición de la figura conservando los ángulos y las distancias entre sus puntos. Este cambio de lugar que se le realiza a la figura está determinado por tres factores:
- Por una magnitud que indica la distancia que hay que desplazar la figura, por lo que, corresponde a la distancia entre el punto inicial y el punto final trasladado.
- Por un sentido que indica hacia donde se está desplazando la figura, por ejemplo, en la imagen de costado ABCDE se desplaza hacia la derecha y luego hacia abajo
- Por una dirección que indica la pendiente con que se realiza el movimiento, por ejemplo, en la imagen ABCDE se desplaza de manera horizontal con una pendiente igual a 0 y luego verticalmente hacia abajo con una pendiente de 90°

Actividad 1 (En el cuaderno)
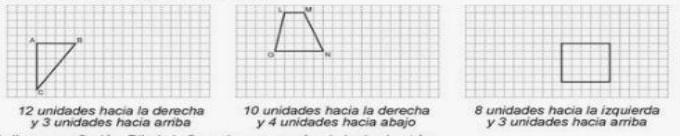
1. Traslada cada figura de acuerdo a las indicaciones
2. Aplica una reflexión: Dibuja la figura imagen según al eje de simetría

3. Ubica los siguiente puntos en el plano: A(3,1) ; B(1,4) ; C(5,1) ; D(3,5)
Luego cada punto trasládalo 3 unidades a la derecha e indica los nuevos pares ordenados correspondientes:
A'( , ) ; B'( , ) ; C'( , ) ; D'( , )
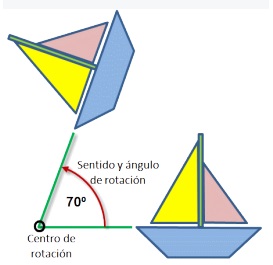
4. Dibuja el barquito en la dirección dada:

La vida cotidiana está llena de situaciones en las que la rotación o giro está presente. Cuando abrimos o cerramos una puerta estamos haciendo una rotación sobre un punto o centro de rotación, las ruedas de nuestra bicicleta giran sobre el eje central, al igual que los pedales, giramos al montar en los caballitos, al abrir y cerrar el abanico hacemos que gire sobre un punto, al mover la ruleta hacemos que gire igualmente sobre su centro.
Cuando se aplica una rotación con respecto al origen de un punto (x, y), se obtiene lo siguiente:
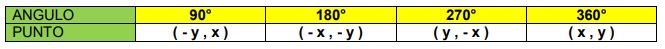
B. Rotación o Giro
Es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original.
Una rotación se determina por estos tres elementos:
- Un ángulo que determina la amplitud de la rotación.
- Un punto llamado centro de rotación.
- Un sentido de la rotación que puede ser del mismo sentido de las agujas del reloj o en sentido contrario.
Por ejemplo, aplicando las relaciones de la tabla anterior para rotar P ( -2,3), se obtienen los siguientes puntos

Actividad 2 (En el cuaderno)
1. Dibuja una Rotación de la figura sobre el eje x (Negativo) y y (Negativo)
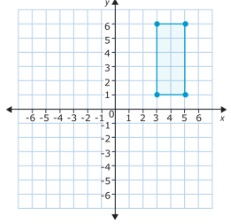
2. Usa esta figura para responder cada pregunta. Siempre que sea posible, escribe todo en notación cartesiana.
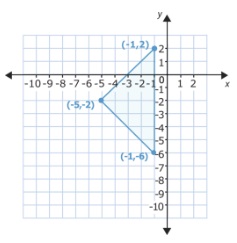
A. Rota esta figura en 180 grados sobre el punto (-1,2).
B. Rota esta figura en 90 (Positivamente) sobre el punto (-1,-6).
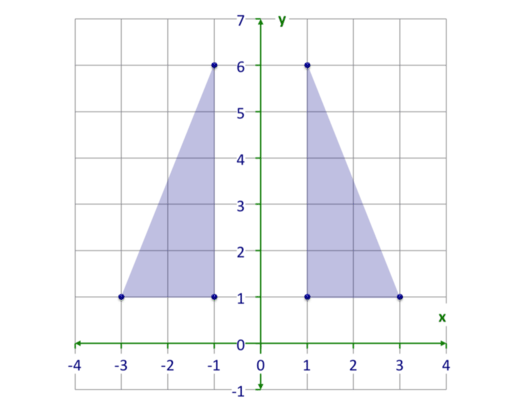
3. Reflexión o Simetría
Una reflexión es una transformación que actúa como un espejo: intercambia todos los pares de puntos que están en lados exactamente opuestos de la recta de reflexión. La recta de reflexión se puede definir con una ecuación o con dos puntos por los que pasa.
Parte 1: reflejar puntos
Estudiemos un ejemplo de reflexión sobre una recta horizontal.
Se nos pide encontrar la imagen A' de A(-6,7) al aplicar una reflexión sobre y=4
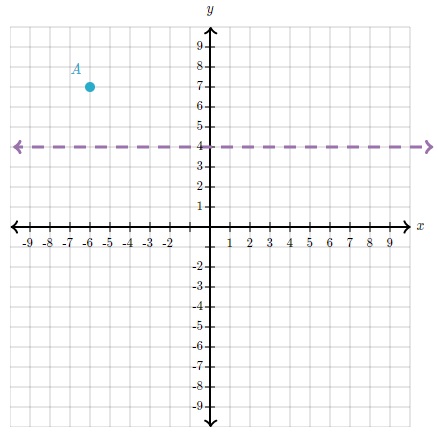
Solución
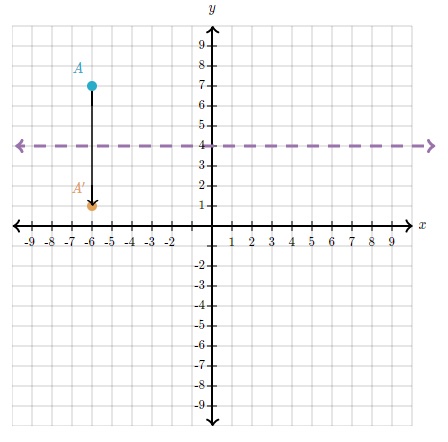
Paso 1: extiende un segmento de recta perpendicular desde A hasta la recta de reflexión y mídelo. Como la recta de reflexión es perfectamente horizontal, una recta perpendicular a ella es perfectamente vertical.
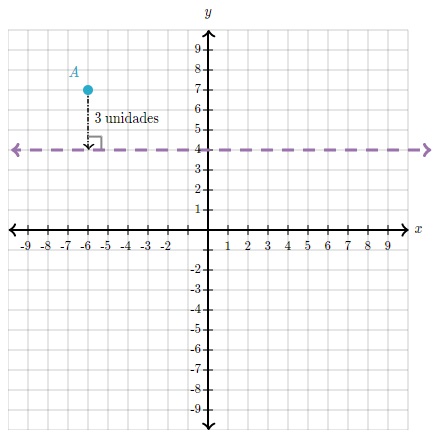
Paso 2: extiende el segmento de recta en la misma dirección y en la misma medida.
Respuesta: A' está en (-6,1)
Estudiemos un ejemplo de reflexión sobre una recta diagonal
Se nos pide encontrar la imagen C' de C(−2,9) aplicar una reflexión sobre y=1 - x
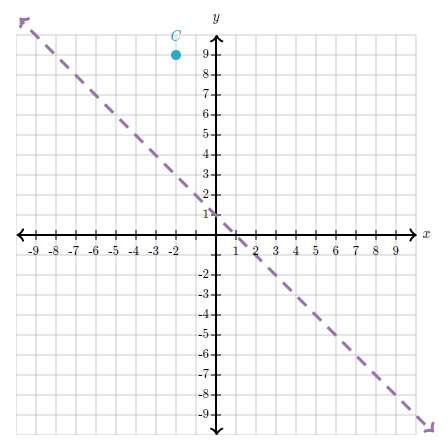
Solución
Paso 1: Extiende un segmento de recta perpendicular desde C hasta la recta de reflexión y mídelo.
Como la recta de reflexión pasa exactamente por las diagonales de los cuadrados unitarios, una recta perpendicular a ella debe pasar por la otra diagonal del cuadrado unitario. En otras palabras, las rectas con pendientes 1 y -1 siempre son perpendiculares.
Por conveniencia, midamos la distancia en "diagonales":
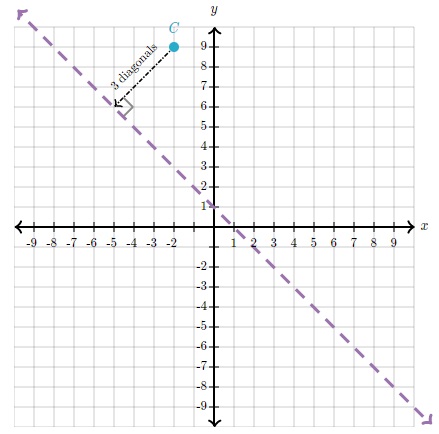
Paso 2: extiende el segmento de recta en la misma dirección y en la misma medida.
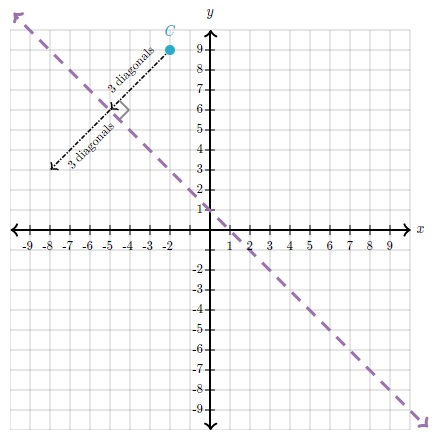
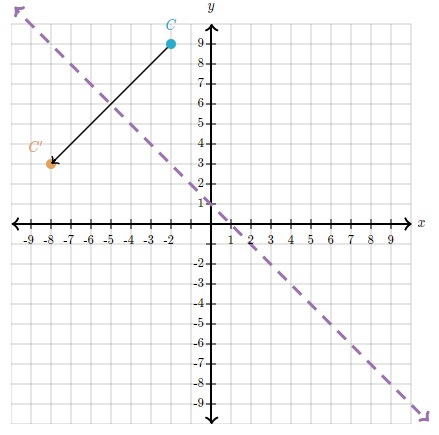
Respuesta: C' está en (-8,3).
Actividad 3 (En el cuaderno):
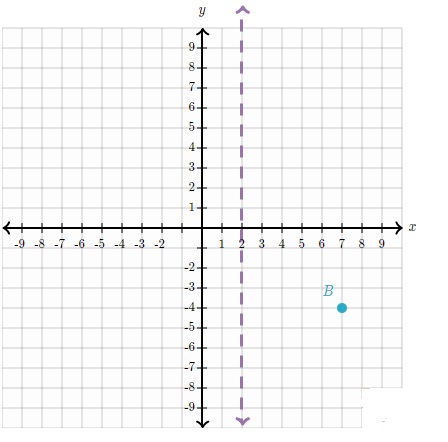
1. Dibuja la imagen de B(7,-4) al aplicar una reflexión sobre x=2
2. ¿Cuál es la imagen de (-25,-33) al aplicar una reflexión sobre la recta y=0?
( , )
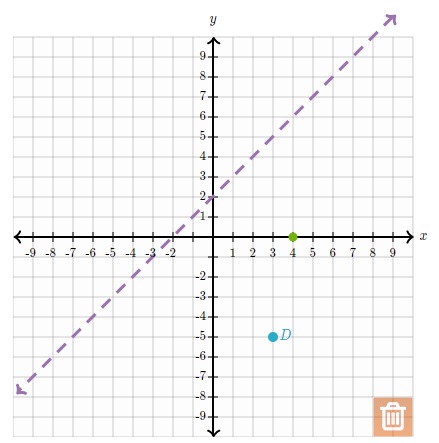
3. Dibuja la imagen de D(3,-5) al aplicar una reflexión sobre y=x+2
4. ¿Cuál es la imagen de (-12,12) al aplicar una reflexión sobre la recta y=x?
( , )
Parte 2: reflejar polígonos
Estudiemos un problema de ejemplo
Considera el rectángulo EFGH dibujado a continuación. Dibujemos su imagen E'F'G'H' al aplicar la reflexión sobre la recta y=x-5.
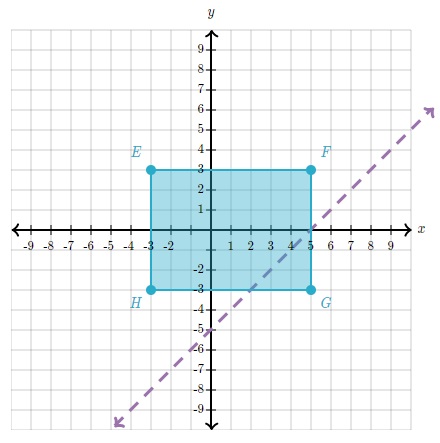
Solución
Cuando reflejamos un polígono, todo lo que necesitamos es realizar la reflexión de todos los vértices (esto es similar a cómo trasladamos o rotamos polígonos).He aquí los vértices fuente y sus imágenes.
Observa que E, F y H estaban sobre el lado opuesto de la recta de reflexión que G. ¡Lo mismo es cierto para sus imágenes, pero ahora cambiaron de lado!
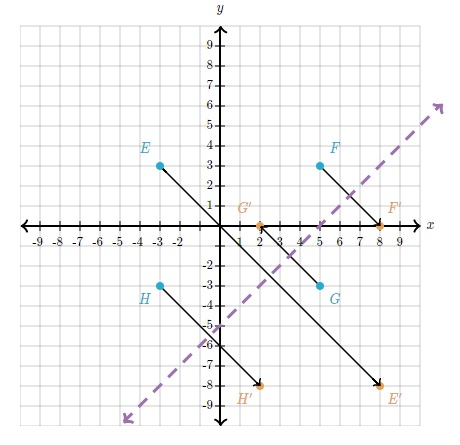
Ahora simplemente conectamos los vértices.
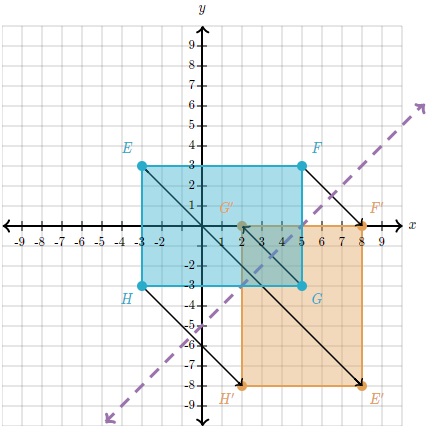
Actividad 4 (en el cuaderno):
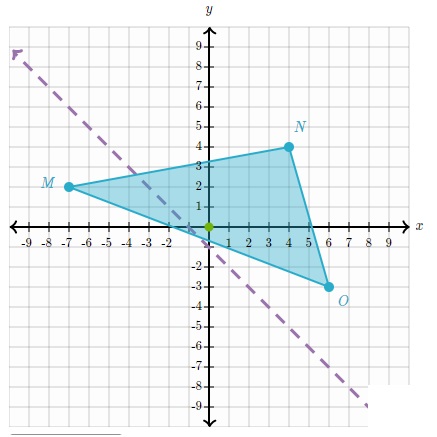
Dibuja la imagen de △MNO al aplicar una reflexión sobre y= -1-x.