Grado 7 P3 - Estadística - Gráficas y medidas de posición

1. GRÁFICAS ESTADÍSTICAS - Ejercicios
En grado undécimo se realizó una encuesta sobre el destino preferido para realizar la excursión de fin de año. En la Siguiente tabla se presentan los resultados obtenidos.

Representa gráficamente en el cuaderno la información:
1. Circular, lineal y en barras
Desarrollo:
Para hacer la gráfica necesitas hallar la frecuencia Relativa vista en el grado 6, para ello tenemos que sumar el total de votos y luego de esto dividir cada resultado de los votos entre el total de votos, luego crear otra columna del porcentaje que contiene los datos de la f.Relativa multiplicada por 100 así:

Para las gráficas lineas y de barras empleamos los datos de la frecuencia absoluta.
1. Gráfica de Barras
Un diagrama de barras se
utiliza para presentar datos cualitativos o datos cuantitativos de tipo
discreto. En el eje horizontal se ubican las variables. En el eje vertical las
frecuencias.

2. Gráfica Circular
Para representar datos de variables cualitativas y cuantitativas discretas también es útil el uso de gráficas o diagramas circulares. Este tipo de diagramas distribuye la superficie de un círculo en sectores de ampliturd proporcional a la frecuencia relativa de cada dato.

3. Gráfica Lineal
Los gráficos o diagramas de líneas muestran un conjunto de puntos conectados mediante una sola línea. Estos gráficos se usan principalmente para mostrar las variaciones de una o más variables estadísticas con respecto al cambio de otra variable, que usualmente es el tiempo.

Ejemplo de gráfica lineal múltiple:
Para poder desarrollar estos gráficos en Excel te dejo el siguiente archivo que podrás descargar:
O en su defecto te dejo un video para que observes el paso a paso de la creación de gráficos:
Actividad 1.
Realizar los ejercicios de la página 189 del libro Vamos a aprender
1. Escribe tres conclusiones que puedas obtener a partir de los gráficos de las siguientes figuras:
Figura1.
a.
b.
c.
Figura 2
a.
b.
c.
2. Representa en un diagrama circular los datos que se muestran en la siguiente tabla correspondientes al número de órganos donados en un país durante el año 2010.

3. Elaborar un diagrama de líneas con las temperaturas promedio de los últimos seis meses del año 2014 en Cali, Medellín y Bogotá que se registran en la siguiente tabla:

4. Construye una tabla en la que se represente el número de personas, el porcentaje y el ángulo correspondiente a cada deporte a partir de los datos del diagrama circular de la siguiente figura. Ten en cuenta que el total de las personas encuestadas es 200.

5. Construye una gráfica circular para mostrar la siguiente información:
Nuestro sistema solar tiene 8 planetas, de los cuales cuatro (04) son de tipo rocoso, es decir, están formados por roca y metal: Mercurio, Venus, Tierra y Marte. Los otros cuatro planetas son de tipo gaseoso, lo que significa que están compuestos por gases muy densos en su atmósfera, a este último tipo corresponden: Júpiter, Saturno, Urano y Neptuno.

Importancia de las medidas de posición estadística
Son el primer paso que debe darse en el análisis descriptivo. Cuando queremos conocer información sobre un fenómeno, comenzamos recopilando datos.
Pero estos, por sí mismos, no nos van a aportar información relevante, por eso hay que analizarlos. Las medidas de posición, junto con las de dispersión, nos ayudan a agruparlos e incluso, a codificarlos.
Estos son el conocimiento principal y básico en estadística. De hecho, las clases universitarias de introducción se centran en ellas. Si no sabemos qué es un promedio, es más que probable que no sepamos entender otros conceptos como la regresión o el contraste de hipótesis.
Por este motivo, es uno de los conocimientos esenciales en ciencias como la económica.
Su cálculo permite analizar los datos en torno a un valor central. Los valores centrales más usados son:
2.1. Media aritmética (Promedio) - X
Es la suma de un conjunto de valores dividida por el número total de ellos. Para hallar la media en un conjunto de datos, basta con sumar todos los datos y dividirlos entre el número total de datos.
La media aritmética es el mismo concepto que conocemos como «promedio».
Ejemplo1
1. Hallar la media aritmética de los siguientes datos 14; 16; 12; 12; 10; 18; 20; 14
Lo primero que hay que hacer es sumar todos los valores que nos dieron, luego se divide entre el número total de datos, en este caso, son 8 datos. Por lo tanto, la media o promedio de esos datos es 14,5.

MEDIDAS
DE TENDENCIA O POSICIÓN CENTRAL
Corresponden a valores que generalmente se ubican en la parte central de un conjunto de datos.
Las medidas de posición son indicadores estadísticos que permiten resumir los datos en uno solo, o dividir su distribución en intervalos del mismo tamaño.
Las medidas de posición, por tanto, sirven para medir y para dividir.
De esta forma, unos resumirán los diferentes valores en uno que, en este caso, sea representativo. Por ejemplo, un promedio. Mientras los otros dividirán el conjunto de los datos en partes iguales, más sencillas de interpretar; estaríamos hablando de los cuantiles.
Ejemplo2:
Dada la tabla de
distribución de frecuencias, calcular la media aritmética.

En este caso, debo tener en cuenta que como tengo la tabla de
frecuencia, los datos están organizados, lo que significa que debo estar atento
y reconocer cuantos estudiantes sacaron la misma nota. Por lo tanto,

La media o promedio es 12,45.
2.2. Mediana (Me)
Es el valor de la variable que deja igual número de datos antes y después de él en una distribución de frecuencia. Si la distribución tiene número impar de datos, la mediana será el valor que quede en el centro, después de ordenar todos los valores de menor a mayor. Si la distribución tiene número par de datos, la mediana se calcula sumando los dos valores que quedan en el medio y dividiendo entre dos.
Ejemplos
1. Halla la mediana de los siguientes datos 6, 10, 7, 8, 13, 11, 9, 12, 14.
Lo primero que hacemos es contar el número de datos, en este caso, son nueve, lo que significa que por ser 9 un número impar, la mediana queda en el centro de la distribución. Luego organizamos los datos de menor a mayor:

Se puede observar que 10 es el número que queda en el centro de los demás, antes quedan cuatro números y después quedan cuatro números, por tanto, 10 es la mediana.
2. Encuentre la mediana del conjunto 3, 10, 36, 255, 79, 24, 5, 8
Organizamos los datos de menor a mayor, nos damos cuenta que son 8 datos, por tanto, debo sumar los dos valores que queden en el medio y dividir entre dos.

Los datos que quedan en la mitad son 10 y 24, por tanto, se suman

17 es la mediana.
2.3. Moda (Mo)
Es el valor de la variable que tiene mayor frecuencia absoluta, en otras palabras, es el dato que más de repite.
Ejemplos
1. Halla
la moda de los siguientes datos: 7; 8; 9; 10; 11; 10; 7; 7
Como la moda es el dato que más se repite, basta con identificar cuál es el valor o el dato que se repite mayor cantidad de veces.
En este caso la moda es 7 porque se repite más veces que los demás datos.

2.
Halla la moda en la siguiente distribución

La variable que tiene mayor frecuencia es 160, por tanto, esa la moda.
Ejemplo general
El profesor Andrés reunió los puntajes de las pruebas de sus estudiantes y obtuvo los siguientes datos:
90, 76, 53, 78, 88, 80, 81, 91, 99, 68, 62, 78, 67, 82, 88, 89, 78, 72, 77, 96, 93, 88, 88.
Encuentra la media, la mediana y la moda de estos datos.
Media
53 + 62 + 67 + 68 + 72 + 76 + 77 + 78 + 78 + 78 + 80 + 81 + 82 + 88 + 88 + 88 + 88 + 89 + 90 + 91 + 93 + 96 + 99 = 1.862

La media o promedio es 80,95
Mediana
53, 62, 67, 68, 72, 76, 77, 78, 78, 78, 80, 81, 82, 88, 88, 88, 88, 89, 90, 91, 93, 96, 99
El dato que queda en el centro es 81, por tanto, es la mediana.
Moda
La moda es el dato que más se repite, por tanto, es 88.
Si te ha quedado alguna duda puedes observar el siguiente video:
ACTIVIDADES
Acción de seguimiento # 1
Resuelve los siguientes ejercicios:
1. Hallar la media aritmética, la mediana y la moda de los siguientes datos, si desean puedes diseñar una tabla.
a. 10, 12, 10, 11, 11, 13, 14, 15, 16
b. 4, 6, 7, 8, 5, 6, 6, 3, 4, 7, 3, 9, 8, 8, 6, 5, 4, 3, 4, 7, 8, 7, 8, 6, 9, 4, 3, 5, 5, 6, 6, 5, 6, 7, 8, 4, 3, 4, 6, 9, 6, 5, 7, 6, 8, 7, 3, 4, 9, 9.
c. 6, 6, 5, 2, 3, 4, 4, 5, 5.
2. Durante el mes de mayo, en Copacabana, se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.c
Hallar la media, la mediana y la moda.
3. Hallar la media, la mediana y la moda de las siguientes tablas

3. EXPERIMENTO ALEATORIO, ESPACIO MUESTRAL, EVENTO Y PROBABILIDAD
3.1. Experimento aleatorio
Es la reproducción controlada de un fenómeno; y cuyo resultado depende del azar.
Ejemplos:
- Lanzamiento de un dado.
- Lanzamiento de una moneda.
Un experimento aleatorio puede ser repetido bajo las mismas condiciones, y se puede describir el número de resultados posibles.
3.2. Espacio muestral (S)
Es el conjunto de todos los resultados posibles de un experimento aleatorio.
- Si se lanza un dado, el espacio muestral está compuesto por los siguientes elementos: S={1, 2, 3, 4, 5, 6}
- Si se lanza una moneda que tiene dos caras: perro (P) y gato (G), el espacio muestral está compuesto por: S={P, G}.
- Si se lanzan dos monedas, el espacio muestral está compuesto por: S={(P, P), (P, G), (G, P), (G, G)}.
- Si se lanza un dado y una moneda, el espacio muestral está compuesto por: S={(1,P),(1,G),(2,P),(2,G),(3,P),(3,G),(4,P),(4,G),(5,P),(5,G),(6,P),(6,G)}
3.3. Evento o suceso
Conjunto de uno o más resultados del experimento aleatorio.
- Si A = {obtener un número 5 al lanzar un dado}, entonces, A={5}.
- Si B = {obtener un número mayor que 3 al lanzar un dado}, entonces, B={4, 5, 6}.
- Si C = {obtener un número par al lanzar un dado}, entonces, C={2, 4, 6}.
- Si D = {obtener al menos 1 gato al lanzar 2 monedas}, entonces, D={(P, G), (G, P), (G, G)}
3.4. Probabilidad
Probabilidad es un valor entre 0 y 1, que indica la posibilidad relativa de que ocurra un evento. El valor de la probabilidad se calcula mediante la siguiente fórmula:
Fórmula de probabilidad en el espacio muestral:

Recuerda que...
- El valor de la probabilidad siempre se encuentra entre 0 y 1 (incluidos ambos números), es decir, 0 ≤ P(A) ≤1.
- La probabilidad de que ocurra un evento imposible es 0. Por ejemplo, la probabilidad de obtener un 8 al lanzar un dado numerado del 1 al 6 es 0, es decir, P(X)=0.
- La probabilidad de que ocurra un evento seguro es 1. Por ejemplo, la probabilidad de obtener un número menor que 7 al lanzar un dado numerado del 1 al 6 es 1, es decir, P(X)=1.
Ejemplo 1:
Calcular la probabilidad de obtener un 2 al lanzar un dado.
Solución:
Vamos a utilizar la fórmula de probabilidad:

El experimento consiste en lanzar un dado. Luego, definimos los resultados o casos del espacio muestral.
S = {1, 2, 3, 4, 5, 6}
Definimos nuestro evento A, como obtener un 2 al lanzar un dado. Ahora, calculamos el número de casos favorables del evento A.
A = { 2 }
Ahora, empleamos la fórmula:


Guía de ejercicios
En la siguiente guía encontrarás muchísimos problemas de probabilidades, algunos de los cuáles, resolveremos juntos en los videos.
Descarga el siguiente archivo y contestar los ejercicios del 1 al 12:
En el siguiente video, vamos a revisar la definición de experimento aleatorio, espacio muestral, evento y probabilidad:
https://www.youtube.com/watch?v=fTIS83G7aC8&feature=emb_logo
4. MEDIDAS DE TENDENCIA O POSICIÓN NO CENTRAL

Las medidas de posición se suelen dividir en dos grandes grupos: la de tendencia no central y las centrales (Que ya vimos). Las medidas de posición no centrales son los cuantiles. Estos realizan una serie de divisiones iguales en la distribución ordenada de los datos. De esta forma, reflejan los valores superiores, medios e inferiores.
Los más habituales son:
4.1. El cuartil:
Los cuartiles son 3 valores de la variable que dividen a un conjunto de datos ordenados en cuatro (04) partes iguales
Se emplean generalmente en la determinación de estratos o grupos correspondientes a fenómenos socio-económicos, monetarios o teóricos.
Los cuartiles representan los valores 25%, 50%, y 75% de los datos.
Los tres cuartiles suelen designarse con los símbolos:
Q1 = primer cuartil
Q2 = segundo cuartil (Coincide con la mediana)
Q3 = tercer cuartil
Ejemplo cuando los datos es impar:
Se tienen las siguientes edades de 11 personas, encontrar los cuartiles:
15 17 16 16 15 17 15 18 14 16 15
1er paso: Ordenar:
14 15 15 15 15 16 16 16 17 17 18
2do Paso:
Hallo primero que todo el cuartil Q2 (mediana)


3er Paso:
Realizamos el mismo proceso al lado izquierdo y derecho de la mediana es decir del número 16

4to Paso: Colocamos 25% al primer término 50% al segundo y 75% al tercero:

Esto significa que el 25% es menor o igual a 15 años, el 50% es menor o igual a 16 años y el 75% es menor o igual a 17 años
La fórmula para hallar la posición de un cuartil en los datos con cifras impar:

Ejemplo1:
Para Nuestro ejemplo vamos a hallar la posición del cuartil No.2 (Mediana)

La posición del segundo cuartil es en la sexta posición (X6)
Ejemplo2:
hallar la posición del cuartil No.3

La posición del tercer cuartil es en la Novena posición (X9)
Ejemplo cuando los datos es par:
Se tienen las siguientes edades de 10 personas, encontrar los cuartiles:
15 16 16 17 17 18 19 19 20 21
Como ya está el primer paso que es ordenar, pasamos al segundo paso que es hallar el cuartil de la mitad, como es par, tomamos los dos del centro y sacamos el promedio:


Para hallar el primer y último cuartil es más fácil por que la cantidad de números (datos) tanto a izquierda como a derecha es impar (5)

La fórmula para hallar la posición de un cuartil en los datos con cifras par:

Ejemplo2:
Para Nuestro ejemplo vamos a hallar la posición del cuartil No.2 (Mediana)

Para hallar el cuartil 1 y 3 empleamos la fórmula de cifras impares:

Antes de realizar la siguiente actividad observa este video donde te explica claramente sobre sobre el cuartil: https://www.youtube.com/watch?v=suSz9RXFNTs
Actividad1:
1. Hallar los 3 cuartiles de los siguientes datos del peso (Kg) de 12 personas
64 56 70 85 55 59 79 62 72 63 60 55
2. Hallar los 3 cuartiles de los siguientes datos número de notas de 13 personas del grado 7:
3,8 3 5 4,2 4,3 2,0 5 5 3,8 2,1 3,5 3,2 4
4.2. El Quintil:
En este caso, divide la distribución en cinco partes. Por tanto, hay cuatro quintiles, cada uno con un valor del 20%. Además, no existe ningún valor que divida la distribución en dos partes iguales. Es menos frecuente que el anterior.
Ejemplo:
Calcular todos los quintiles de las siguientes muestras de notas en matemáticas de un aula (notas de 0 a 20):
16 10 12 8 15 18 20 9 11 1 13 17 9 10 14
1er Paso: Ordenar
1 8 9 9 10 10 11 12 13 14 15 16 17 18 20
2do Paso: Dividimos el número de datos entre 5
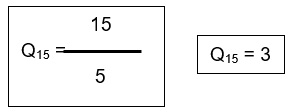
Es decir, separamos grupos de a 3:

3er Paso: Colocamos el intervalo del quintil
Fórmula:
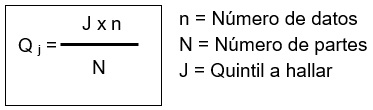
Ejemplo:
Hallar la posición del 1er y último quintil:
Primer Quintil: Ultimo Quintil:

4to Paso:
Colocar los intervalos:
Intervalo: [1,3] Intervalo: [10,12]
Para tener mayor conocimiento sobre el tema, puedes observar el siguiente video:
Actividad 2:
Hallar el quintil de las siguientes edades en las que se contrae matrimonio ya ordenadas
18 18 23 27 28 30 31 32 32 33 33 34 34 38 42
4.3. El Decil:
Son medidas de posición, Son 9 valores D1 a D9 que dividen el conjunto de datos ordenados en 10 partes iguales. El D5 se corresponde con la mediana (Me).
Sus valores van del 10% hasta el 90%
Ejemplo:
Tenemos las notas de 20 estudiantes ya ordenados:
25 28 30 30 35 35 36 37 37 38 40 40 40 40 40 40 41 43 48 50

y 20/10 = 2, es decir cada 2 posiciones se forma un Quartil

Salieron 10 Conjuntos de a dos datos.
Vamos a hallar el decil Número 4 (D4), para ello utilizamos la fórmula anterior de posición,

Comenzamos a contar desde el inicio ocho (08) posiciones:

Significa que el 40% de los estudiantes sacó 3,7 o menos
Para tener mayor conocimiento sobre el tema, puedes observar el siguiente video:
Actividad 3:
Hallar el quintil de
las siguientes notas del grado 7 ya ordenadas

Nota: Cuando un decil me da fraccionado, por ejemplo 4,5 tenemos que sacar el promedio de los números que están en la posición 4 y la posición 5.
4.4. El Percentil:
Por último, este cuantil divide la distribución en cien partes. Es decir, van a haber 99 percentiles. Es útil si queremos separar nuestros datos más detalladamente. Como hay tantos percentiles ya no es tan obvio ubicarlos. Para ello es más factible utilizar la fórmula
Primero que todo vamos a hallar i, que va a ser el numero de datos (n) por el percentil que nos interesa (k).
i = n . k, Si n . k nos da un número entero, entonces:

Si i nos da un número no entero, utilizamos la siguiente fórmula:
Pk = Tomamos el siguiente entero después de i.
Ejemplo1:
Para ello vamos a utilizar la siguiente tabla con 24 datos

De esta tabla halla el percentil No.47.
Respuesta:
i = 24 (datos) . 0.47 (Porcentaje) = 11,28 (El número no es entero)
Entonces tomamos como i el siguiente número entero que es 12.
Por lo tanto, la posición del percentil va a ser 12. P47 = Posición 12

Ejemplo2:
Hallar el percentil 75
i = 24 . 0.75 = 18 (Entero)
Como nos dio un entero entonces utilizamos la siguiente fórmula:

¿Cuál es la posición 18,5?

Por lo tanto, sacamos el promedio de los dos números:

Nota: El percentil 25 = 1er cuartil
El percentil 50 = 2do cuartil = Mediana
El percentil 75 = 3er cuartil
Si quieres reforzar el tema, te invito a ver el siguiente video:
Actividad4:
En grupos de 4 se van a distribuir los temas de quintil, decil y percentil, van a preparar exposición a sus compañeros y van a grabar la exposición que puede ser magistral o mediante diapositivas.
Si quieres descargar la guía lo puedes hacer aqui:
