Grado 7 P3 - MATEMÁTICAS - Razones y proporciones

1. RAZONES Y PROPORCIONES
A. RAZONES: (11/07/2022)
Es una expresión numérica de comparación entre las medidas de dos magnitudes. La razón entre a y b se escribe a/b ó a:b, y se lee "a es a b"
EJEMPLO: La relación entre el número de profesores y el número de estudiantes que existe en la I.E.Jesús Antonio Amézquita sede Santafé se puede expresar con la razón matemática: 7/120, 7:120 donde se puede concluir que por cada profesor hay 17 alumnos aproximadamente.
En una razón se pueden
identificar dos términos:

VIDEO:
El ejemplo de proporcionalidad lo encontramos en el teorema de Tales: Observa el siguiente video para comprobarlo: https://www.youtube.com/watch?v=staL7w-eT58
Video sobre proporciones:
JUEGOS:
Realiza la siguiente actividad interactiva (Juegos):
https://wordwall.net/es/resource/14048429/razones-y-proporciones
ACTIVIDAD1
1. Expresa los enunciados mediante una razón:
a. Dos carros por cada apartamento
b. Cuatro naranjas por cada 6 peras
c. Tres galletas por cada 2 panes
d. Dos pantalones por cada 3 camisas
e. Tres mujeres por cada hombre
2. Encuentra dos razones equivalentes a cada una de las razones dadas:

3. Halla el antecedente de las razones, si el coeficiente de proporcionalidad de cada una es igual a 0,6.

4. Determina si la razón 38/4 forma una proporción con cada una de las siguientes razones.

5. Identifica los extremos y los medios de cada proporción. Luego, halla el coeficiente de proporcionalidad en cada caso.

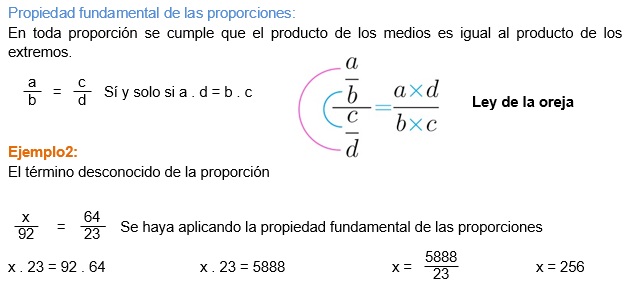
6. Haya el valor desconocido de cada proporción.

2. MAGNITUDES CORRELACIONADAS

En el año 2014 se consideraba que la producción de leche en Colombia registraba costos muy altos.
En la siguiente tabla muestra el costo de producción:

¿Cómo se relacionan las magnitudes presentadas en la tabla?
2.1. Magnitudes directamente correlacionadas
Las magnitudes que están relacionadas en el anterior ejemplo son el número de litros de leche y su costo de producción. Cuando el número de litros aumenta el costo también; por tanto se dice que entre las dos magnitudes existe una correlación directa.
Dos relaciones A y B están directamente correlacionadas, si al aumentar A también aumenta B, o al disminuir A también disminuye B.
Ejemplo:
En la tabla se muestra
la relación entre la longitud del lado de un triangulo equilátero y su perímetro. Estas magnitudes tienen una correlación directa, ya que a medida que aumenta la longitud
del lado, aumenta el perímetro del triángulo.
2.2. Magnitudes inversamente correlacionadas
Así como hay magnitudes directamente correlacionadas también se puede también se pueden encontrar magnitudes inversamente correlacionadas.
Dos relaciones A y B están inversamente correlacionadas, si al aumentar A disminuye B, o viceversa.
Ejemplo1:
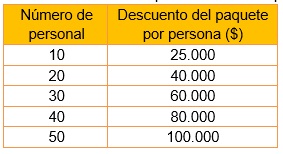
Las magnitudes de la siguiente tabla están inversamente correlacionadas, ya que a medida que aumenta el número de personas el costo por paquetes turístico disminuye.

Ejemplo2:
Las magnitudes de la siguiente tabla están directamente correlacionadas, ya que a medida que aumenta el número de personas el costo por paquetes turístico aumenta.
ACTIVIDAD2
1. Determinar si cada par de magnitudes están correlacionadas. En caso afirmativo, escribe si la correlación es directa o inversa.
- Altura de un edificio y número de personas que lo habitan.
- Velocidad de un auto y tiempo que tarda en frenar
- Número de habitantes de una población y densidad demográfica en el pueblo
- Número de obreros para construir un edificio y tiempo que tardan en terminar la obra.
- Capacidad de una botella y número de botellas que se necesitan para envasar cierta cantidad de líquido.
- Número de vas lecheras y cantidad de litros de leche producida.
- Número de trabajadores y tiempo que emplean en hacer una obra.
2. Califica como falso (f) o verdadero (v) cada una de las afirmaciones.
Si dos magnitudes están directamente correlacionadas, entonces al duplicar una la otra también se duplica. ( )
Si una magnitud es constante, no puede estar correlacionada con ninguna magnitud. ( )
Dos magnitudes no pueden estar correlacionadas de forma directa e inversa simultáneamente. ( )
3. Decide cuál de las siguientes gráficas representa magnitudes correlacionadas y explica por qué?

3. PROPORCIONALIDAD DIRECTA

Laura publicará un libro de recetas. Para mostrar la relación entre la cantidad de ingredientes y el número de porciones, incluirá gráficas y tablas. La siguiente tabla acompañará la receta para elaborar un ponqué.

¿Qué tipo de relación presenta tales magnitudes?
En la anterior tabla se observa que al aumentar el número de porciones aumenta el número de huevos. Además, cuando se calcula la razón entre el número de porciones y el respectivo numero de huevos se tiene que:

Por tanto, como las magnitudes están directamente correlacionadas y el cociente entre las cantidades correspondientes de las magnitudes es constante e igual a 4, se dice que las magnitudes son directamente proporcionales y el cociente 4 es la razón de proporcionalidad.
Dos magnitudes son directamente proporcionales si están directamente correlacionadas y el cociente entre cada para de valores correspondientes de las magnitudes es constante.
Ejemplo:

En la siguiente
tabla se registran las distancias recorridas por un automóvil que viaja a velocidad constante en diferentes intervalos de tiempo.
Estas magnitudes son directamente proporcionales, y su correspondiente
representación gráfica se muestra en la figura lineal:

La razón entre la distancia y el tiempo es la velocidad
Entonces como:

Se dice que la velocidad constante del automóvil durante el recorrido fue de 70 Km/h
ACTIVIDAD3
1. Halla la razón de proporcionalidad de cada par de magnitudes directamente proporcionales y completa la tabla respectiva.



4. PROPORCIONALIDAD INVERSA

El día de los niños José visita una fundación de menores de bajos recursos a la que normalmente asisten 75 de ellos. José había comprado 150 naranjas para ofrecer dos a cada uno, pero ese día la directora le dice que solo asistieron 50 niños.
Si José quiere repartir las 150 naranjas entre los niños que asistieron, ¿Cuántas le corresponden a cada uno?
A. Magnitudes inversamente proporcionales
Entre menos niños asistan a la fundación, más naranjas le corresponderán a cada uno. Esto indica que las magnitudes número de niños y cantidad de naranjas están inversamente correlacionadas. En la siguiente tabla se registran los datos que suministra el problema.

El producto del número de niños por la cantidad de naranjas que recibe cada uno
debe ser igual a la cantidad total de naranjas que compró José, es decir, 150. Así que:

Entonces a cada niño le corresponden tres (03) naranjas.
Dos magnitudes A y B son inversamente proporcionales si están inversamente correlacionadas y se verifica que:

a . a' = b . b' = c . c'..... = k, siendo k la razón de proporcionalidad.
Ejemplo:
La velocidad y el tiempo son magnitudes inversamente proporcionales, pues a mayor velocidad empleada para recorrer una distancia el tiempo que se invierte en el recorrido es menor. En la tabla se observa la relación entre tales magnitudes al recorrer una distancia constante de 60 Km.

De los datos de la tabla se infiere que:
60 . 1 = 30 . 2 = 20 . 3 = 10 . 6 = 60
Por tanto 60 es la razón de proporcionalidad, la relación entre las magnitudes se representa en la siguiente figura:

ACTIVIDAD4
1. Representa gráficamente las magnitudes inversamente proporcionales que se muestran en las siguientes tablas:

2. Halla la constante de proporcionalidad inversa en cada caso y completa las tablas:

5. REGLA DE TRES SIMPLE


Juliana prepara Brownies para la celebración de cumpleaños de su padre a partir de la receta que encontró en un libro de cocina.
Las magnitudes, números de porciones y cantidad de ingredientes son directamente proporcionales. Por tanto, para determinar la cantidad de ingredientes que debe usar Juliana en la preparación de doce browinies si se conocen los ingredientes para ocho porciones, se debe plantear una proporción por cada ingrediente y luego hallar el término desconocido, como se muestra en la tabla.

Ejemplo:
¿Si ocho (08) porciones de queso poseen 400 Calorías, cuantas calorías poseen 35 porciones?
En esta situación las magnitudes números de porciones y calorías son directamente proporcionales, sabiendo esto se
puede responder la pregunta a partir del siguiente procedimiento (Se relacionan los datos en una tabla) :


ACTIVIDAD5
Escribe la proporción correspondiente a cada situación propuesta.
- ¿Si un pasaje de Rioblanco a Bogotá cuesta $112.000, cuánto cuestan 5 pasajes?
- Un automóvil recorre 48 Km en 35 minutos. ¿Cuantos kilómetros recorre en una hora?
- La temperatura de un horno sube 2 °C cada cinco minutos ¿Cuánto ha subido la temperatura al cabo de una hora?
- Para cocinar una taza de arroz se emplean dos de agua. ¿Cuántas tazas de arroz se cocinaron si se usaron diez de agua?
- En el salón de clases del grado Séptimo por cada seis niñas hay nueve niños. Si hay 18 niñas, ¿Cuántos niños hay?
6. REGLA DE TRES COMPUESTA


El director de una obra ha establecido que, para levantar doce paredes, contratando ocho obreros gasta diez días. ¿Cuánto tiempo empleará para levantar 30 paredes, contando con diez obreros?
Para resolver este problema es necesario utilizar una regla de tres compuesta, el cual sigue los siguientes pasos:
1. Reunir los datos de acuerdo a sus magnitudes:
Se puede decir que las magnitudes x, y, z se pueden relacionar con las siguientes razones (z es la magnitud que contiene el dato desconocido o variable):

Para nuestro ejemplo se plantea una razón para cada una de las magnitudes involucradas en la situación:

2. Con base en los datos, se puede plantear la ecuación que permite resolver un problema que involucre la regla de tres compuesta así:
a. Si la magnitud Z (Donde se ubica la variable a encontrar) es directamente proporcional a las magnitudes X, Y entonces

b. Si la magnitud Z (Donde se ubica la variable a encontrar) es inversamente proporcional a las magnitudes X, Y entonces

c. Si la magnitud Z (Donde se ubica la variable a encontrar) es directamente proporcional a la magnitud X, e inversamente proporcional a la magnitud Y
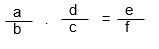
Para nuestro caso se determina la relación entre cada una de las dos primeras magnitudes con la tercera magnitud (Z) que es la que contiene la incógnita.
- Las magnitudes tiempo de la obra (Z) y cantidad de paredes (X) son magnitudes directamente proporcionales. (Entre más tiempo más paredes se pueden construir)
- Las magnitudes tiempo de la obra (Z) y cantidad de obreros (Y) son magnitudes inversamente proporcionales. (Entre más obreros menos tiempo se va a gastar)

ACTIVIDAD6
1. Determina la relación de proporcionalidad existente entre cada par de magnitudes en cada caso.
a. Área del piso - Cantidad de baldosas - tiempo de embaldosado
b. Velocidad - distancia recorrida - tiempo empleado
c. Cantidad de líquido en un tanque - cantidad de grifos que suministran líquido - tiempo de llenado.
d. Cantidad de líquido en un tanque - Cantidad de grifos que suministran líquido - tiempo de llenado
e. Cantidad de dinero recaudado - número de provisiones - valor de cuota por persona.
2. Analiza cada esquema y realiza las actividades:


- Redacta el enunciado y la pregunta que sugiere cada uno de los esquemas planteados
- Analiza la relación que existe entre la magnitud a la que corresponde la incógnita y las otras dos magnitudes.
- Plantea la ecuación que relacione las tres variables y desarróllala.
AUTOEVALUACION COMPONENTE HACER Y SER - CONVIVIR
(La realiza el estudiante)
