Grado 8 P3 - Geometría - Triángulos (Mediana, Altura, Bicectriz, Mediatriz, Perímetro, Área, Semejanza y Congruencia)
RECORDEMOS:
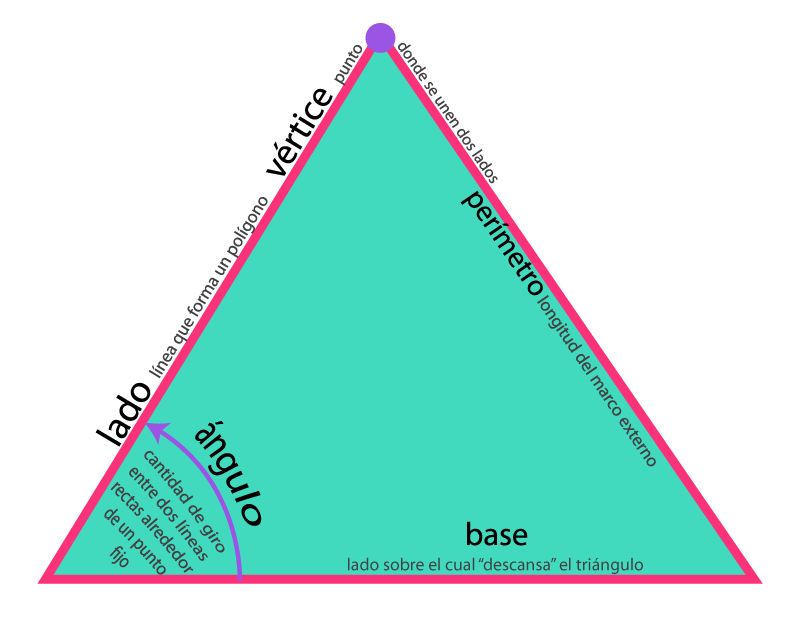
1. El perímetro de un polígono (o cualquier otra curva cerrada) es la distancia alrededor del exterior. El perímetro es medido en unidades lineales
2. El área de una curva simple, cerrada, plana es la cantidad del espacio interior. El área es medida en unidades cuadradas
3. El volumen de un sólido de forma 3D es la cantidad del espacio desplazado por él. El volumen es medido en unidades cúbicas
PUNTOS Y LINEAS NOTABLES DE UN TRIÁNGULO
1. MEDIANA
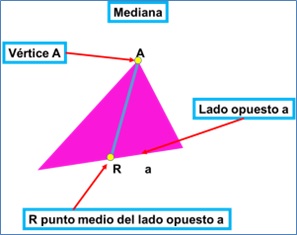
Mediana. Es el segmento trazado desde un vértice hasta el punto medio del lado opuesto.
Hay tres medianas que corresponden una a cada lado. Se les designa con la letra «m» y un subíndice que indica el lado.
El punto donde se cortan las tres medianas se llama baricentro.
2. ALTURA
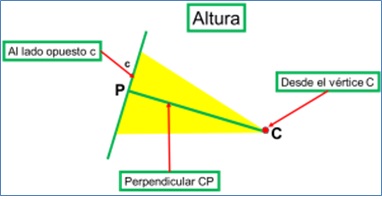
Altura. Es la perpendicular trazada desde un vértice, al lado opuesto o a su prolongación (Formando 2 ángulos de 90°).
Hay tres alturas, una correspondiente a cada lado. Se designan con la letra «h» y un subíndice que indica el lado. El punto donde intersectan las tres alturas se llama ortocentro.
3. BISECTRIZ
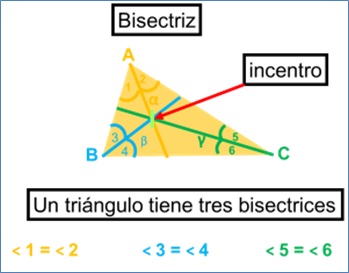
Bisectriz. Es la recta que corresponde a la bisectriz de un ángulo interior (divide al ángulo en dos ángulos iguales).
Hay tres bisectrices, una para cada ángulo; se nombran generalmente con las letras griegas alfa, beta y gamma.
El punto donde concurren las tres bisectrices se llama incentro.
4. MEDIATRIZ

Mediatriz. Es la perpendicular en el punto medio de cada lado.
Hay tres mediatrices que se denominan con la letra «M» y un subíndice que indica el lado.
El punto de intersección de las tres mediatrices se llama circuncentro.
La suma de los tres ángulos interiores de un triángulo es igual a 180°
Si no te quedó claro el tema te invito a que observes la siguiente página:
También podrás observar el siguiente video:
Actividad1:
1. Realizar la actividad de la dirección electrónica que está a continuación y enviar el pantallazo del resultado de la evaluación vía wp.
https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/ejercicios-interactivos-de-alturas-medianas-mediatrices-y-bisectrices.html
2. Hallar el baricentro, ortocentro, incentro y circuncentro de la siguiente figura (Todas por aparte en el cuaderno):

5. PERÍMETRO Y AREA DE UN TRIÁNGULO
El Perímetro de un triángulo es igual a la suma de todos sus lados.
A. Perímetro: Suma de sus tres lados.
Si el triángulo es equilátero, como sus lados (l) son iguales, sería 3l.
En el caso de que fuese Isósceles, dos lados iguales uno distinto, sería 2l+b.


Ejemplo:
Hallar el área del triángulo cuyos lados miden 3, 4 y 5 cm
Lo primero que hacemos es hallar el perímetro: P = 3 Cm + 4 Cm + 5 Cm = 12 Cm
Reemplazamos en la formula:
Si no te quedo claro el tema sobre perímetro y área de un triángulo y la fórmula de Herón, te invito a observar el siguiente video:
ACTIVIDAD3:
1. Hallar el área del siguiente triángulo utilizando la fórmula de Herón:

2. Realizar la evaluación en línea de la página: (Enviar pantallazo al docente vía wp)
https://wordwall.net/es/resource/20580262/prueba-%C3%A1rea-y-per%C3%ADmetro
6. SEMEJANZA Y CONGRUENCIA
Objetivo de la unidad:
1. Clasificar transformaciones de figuras.
2. Evaluar la congruencia de las figuras.
3. Interpretar la semejanza de las figuras.
4. Justificar los teoremas de triángulos.

Cuando pensamos en la forma y el tamaño de las figuras geométricas, consideramos la posibilidad de que algunas de ellas coincidan con otras. Por ejemplo, las hojas de un árbol son aproximadamente iguales o parecidas entre sí. La Geometría establece maneras de trabajar con estas coincidencias mediante los conceptos de congruencia y semejanza.

La congruencia y la semejanza de las figuras son conceptos fundamentales de la geometría euclidiana. Las figuras congruentes son idénticas mientras que, si son semejantes, estas tienen ángulos de igual medida y lados correspondientes en la misma proporción. Decimos que las figuras congruentes son semejantes pero las figuras semejantes no son necesariamente congruentes.
6.1. SEMEJANZA

6.1.1. Teorema de la semejanza LLL (Lado, Lado, Lado):
Si los tres lados de un triángulo son proporcionales a los tres lados de otro triangulo, entonces los dos triángulos son semejantes.
6.1.2. Teorema de la semejanza LAL. (Lado, Ángulo, Lado)
Si un ángulo de un triángulo es congruente con el ángulo de otro triangulo, y si los lados correspondientes que incluyen al ángulo son proporcionales, entonces los triángulos son proporcionales.
6.2. CONGRUENCIA

Triángulos congruentes
Dos triángulos son congruentes si hay una correspondencia entre sus vértices de manera que cada par de lados y ángulos correspondientes sean congruentes. Obsérvese que la congruencia puede definir de manera similar para otras figuras.
Definición:
Congruencia: Que tiene la misma medida.
Símbolo: (Ξ) Ej: AB≡CD
Teorema y postulados:
Teoremas:
6.2.1. Teorema de congruencia LLL (lado - lado - lado)
Si tres lados de un triángulo son congruentes con tres lados de un segundo triangulo, entonces los dos triángulos son congruentes.
6.2.2. Teorema de congruencia LAL (lado - ángulo - lado)
Si dos lados y el ángulo incluido de un triángulo son congruentes a dos lados y el ángulo incluido de un segundo triangulo, entonces los dos triángulos son congruentes
6.2.3. Teorema de congruencia ALA (ángulo - lado - ángulo)
Si dos ángulos y el lado incluido de un triángulo son congruentes con dos ángulos y el lado incluido de un segundo triangulo, entonces los dos triángulos son congruentes.
Postulados:
6.2.4. Postulado (ALA)
Si dos ángulos y el lado incluido de un ∆ son ≡ a los ángulos y el lado incluido de otro∆, entonces los triángulos son congruentes

6.2.5. Postulado (LLL)
Si tres lados de un ∆ con congruentes respectivamente a tres lados de otro ∆ entonces los triángulos son congruentes.

6.2.6. Postulado (LAL)
Si dos lados y el ángulo incluido de un triángulo son congruentes a dos lados y al ángulo incluido de otro triángulo, entonces los triángulos son congruentes.
Ejemplo:

Repaso de teoremas de congruencia
Tal como lo has estudiado en lecciones previas, existen Siete (07) teoremas y postulados que te proporcionan diferentes caminos para probar que dos triángulos son congruentes sin tener que revisar todos los ángulos y lados de ambos. Es importante conocer muy bien estas siete reglas, de manera que puedas utilizarlas en aplicaciones prácticas

Si no te quedó claro el tema de semejanza y congruencia, te invito a observar los siguientes videos:
ACTIVIDAD4:
1. ¿Cuál regla puede probar que los triángulos que siguen son congruentes?
2. ¿Cómo podrías demostrar que △ABC≅△DEC en el diagrama de abajo?
3. En el siguiente diagrama, Midtown se encuentra exactamente a mitad de camino entre Uptown y Downtown. ¿Cuál es la distancia entre Downtown y Lower East Side? ¿Cómo la determinaste? Escribe algunas breves líneas para convencer al lector de que tu respuesta es correcta.
4. Desarrolla la actividad interactiva en el siguiente link (Envía pantallazo evidencial de tu calificación vía wp)
https://wordwall.net/es/resource/31458928/matem%c3%a1ticas/congruencia-de-tri%c3%a1ngulos
