Grado 8 P3 - Matemáticas - Factorización

1. EXPRESIONES ALGEBRAICAS
Es una combinación de cantidades numéricas y literales, relacionadas por las operaciones de suma, resta, multiplicación, división, potenciación y radicación. Las letras reciben el nombre de variables.
Ejemplo:
Las siguientes expresiones son algebraicas:

1.1. Tipos de expresiones algebraicas:
a. Expresiones algebraicas enteras: En ellas intervienen las operaciones básicas y los exponentes de las variables son números enteros positivos.
b. Expresiones algebraicas fraccionarias: Tienen algunas variables en el denominador.
Ejemplo:

C. Expresiones algebraicas irracionales: Contienen expresiones radicales en sus términos o variables con exponente racional no entero
Ejemplo:

1.2. Valor numérico de una expresión algebraica
Es el resultado que se obtiene de sustituir la parte literal de la expresión algebraica por números determinados y aplicar las operaciones indicadas en la expresión.
Ejemplo:

Sino te quedó claro el tema observa el siguiente video:
Actividad 1
1. Escriba las expresiones algebraicas correspondientes a cada uno de los anunciados:

2. Determinar el valor numérico de las siguientes expresiones algebraicas sabiendo que:
x = -2, y = 3, z = 4

3. La energía potencial está dada por la expresión Ep = mgh, donde m es la masa, g es la gravedad (g=9,8 m/s2) y h la altura
Según esta información completa la tabla

4. Ve al siguiente link y realizar el juego en linea y al terminar envía el pantallazo al docente:
https://www.cerebriti.com/juegos-de-matematicas/o-expresiones-algebraicas

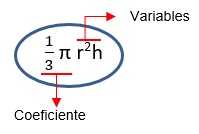
2. Monomio
Es una expresión
algebraica que consta de un solo término, formado por el producto de números
reales y las potencias de exponente entero positivo de una o más variables.
2.1. Elementos de un monomio
Un monomio está formado por:
- Un coeficiente, que es la parte numérica
- Una parte literal o variable, constituida por las variables y sus exponentes naturales.
El grado absoluto de un monomio corresponde a la suma de todos los exponentes de las variables.
Si dos o más monomios tienen el mismo grado absoluto, son homogéneos. De lo contrario, son heterogéneos.

2.2. Monomios Semejantes
Si los monomios tienen la misma parte literal (Variables), se dice que son monomios semejantes. Por lo tanto, dos monomios semejantes solo se diferencian en los coeficientes.

Para afianzar el tema observa el siguiente video:
https://www.youtube.com/watch?v=iPZRUuyUp8o
Actividad2:
Realizar los ejercicios en el siguiente link sobre monomio. Al terminar envía el pantallazo con la calificación al docente por el WP.
https://www.superprof.es/apuntes/escolar/matematicas/algebra/polinomios/ejercicios-de-monomios.html

3.1. Diferencia de cuadrados
La diferencia de dos cuadrados es un teorema que nos dice si es que una ecuación cuadrática puede ser escrita como un producto de dos binomios, en donde uno muestra la diferencia de las raíces cuadradas y el otro muestra la suma de las raíces cuadradas.
3. Factorización de Binomios
Estándar:
En esta guía se analizarán los
procedimientos, que se pueden usar con un binomio para ser factorizado, tales
como la diferencia de cuadrados, suma o diferencia de potencias iguales y suma o
diferencia de cubos.

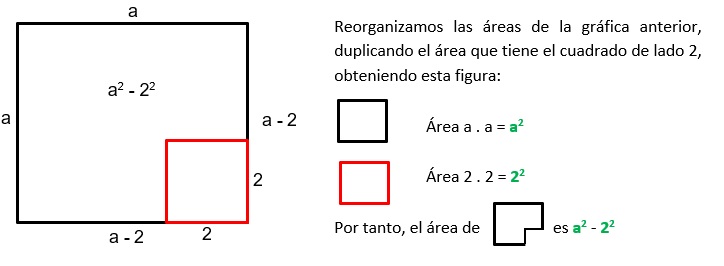
3.1.1. Representación gráfica:
Lo representaremos gráficamente para ver el proceso que se realiza desde el trabajo con áreas, es decir, representamos un cuadrado de lado a, en el cual dividimos un cuadrado de lado 2.
3.1.2. Fórmula:
La fórmula de la diferencia de cuadrados es una forma algebraica que es usada para expresar la diferencia entre dos valores elevados al cuadrado. Una diferencia de cuadrados es expresada en la forma:






Si quieres reforzar el tema de Factorización por diferencia de cuadrados, observa el siguiente video:
Actividad3:
1. Factoriza los siguientes ejercicios, con la ayuda de un compañero:


3. Ingresa al siguiente link y juega sobre el tema (No se te olvide enviar el pantallazo al wp del grupo):
https://www.cerebriti.com/juegos-de-matematicas/factorizacion-diferencia-de-cuadrados
3.2. Cubo perfecto de Binomio

También llamado Un binomio al cubo o cubo de un binomio (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
Ejemplo:

Paso1: Verificar si esta expresión cumple con las condiciones para ser considerada como cubo de un binomio:
a. Tiene cuatro términos
b. Dos términos (el primero y el último) son cubos perfectos, es decir existe su raíz cubica dentro del conjunto de los Enteros.
c. El segundo término es tres veces el producto de la primera raíz elevada al cuadrado por la segunda raíz elevada a la potencia uno.
d. El tercer término es tres veces el producto de la primera raíz elevada a la potencia de uno por la segunda raíz elevada al cuadrado.

Paso2: Se hallan las raíces cubicas de los términos, primero y último, se verifica si los términos son positivos se establece una adición entre los mismos, en caso de presentarse los signos positivos y negativos de forma intercalada, entonces se establece una sustracción.

Si no entendiste el tema "Cubo perfecto de binomios" te invito a observar los siguientes video:

2. Ingresa al siguiente link y desarrolla el juego. Al terminar envía el pantallazo al Whatsapp del grupo.
https://www.cerebriti.com/juegos-de-matematicas/encuentra-el-cubo-perfecto-de-un-binomio
3.3. Suma o diferencia de cubos perfectos

La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.
La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces
cúbicas, y el segundo se compone del cuadrado de la primera raíz más el
producto de ambas raíces más el cuadrado de la segunda raíz.

Ejemplo1:
Paso1: Hallamos la raíz cúbica de los dos términos dados, en la expresión algebraica.
Nota: Si es una suma de cubos perfectos se desarrolla de la siguiente manera:
Se construye con la adición de las raíces cúbicas de
los términos dados.
Paso2:
El segundo paréntesis se conforma con la primera raíz cúbica elevada al cuadrado, más el producto de las raíces cúbicas, más la segunda raíz elevada al cuadrado.


Paso2:
El segundo paréntesis se conforma con la primera raíz cúbica elevada al cuadrado, menos el producto de las raíces cúbicas, más la segunda raíz elevada al cuadrado.

Si no comprendiste el tema te invito a observar el siguiente video:
Actividad 4:
Realizar Los siguientes ejercicios utilizando suma o diferencia de cubos perfectos:
5. Desarrolla la actividad interactiva (Juego) y al finalizar tómale un pantallazo y envíalo al grupo de WP.
https://es.educaplay.com/recursos-educativos/4656422-suma_y_diferencia_de_cubos.html
4. Factorización de trinomios
En esta guía se analizará el procedimiento que es aplicable a una
expresión algebraica como los trinomios, para ser factorizados, a través de los
casos de trinomio cuadrado perfecto, trinomio de la forma x2 + bx+ c, trinomio de la forma ax2 + bx+ c, ó trinomio por adición y sustracción.
4.1. Trinomio Cuadrado Perfecto

Es un trinomio que resulta de la multiplicación de un binomio por sí mismo o elevado al cuadrado.
4.1.1. Explicación gráfica:
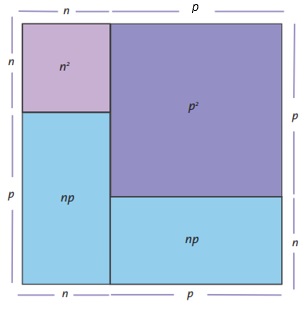
Aplicaremos en principio el desarrollo geométrico para ver el manejo desde las áreas.
1. Esta expresión algebraica, nos entrega las siguientes figuras geométricas que constituyen las áreas, si bien es cierto que desde la expresión sólo se tienen tres términos, es necesario aclarar que al tener dos veces el área np, se presentan dos veces la misma fi gura geométrica, de ahí que resulten cuatro cuadriláteros.

2. Reorganizando las figuras geométricas, es posible armar el siguiente cuadrado:
3. El cuadrado que se obtiene tendría de lado, n + p, luego su área es Esta reconfiguración es posible expresarla como:

4.1.2. Explicación algebraica:
Procedimientos:
Paso1: Hallamos la raíz cuadrada de los dos términos que son cuadrados perfectos.
Paso2: Verificamos que tenga la conformación de trinomio cuadrado perfecto, es decir el segundo término debe ser dos veces el producto de las raíces y los dos términos restantes deben estar elevados al cuadrado.
Paso3: Si todos los términos son positivos, entonces se entrega un paréntesis que contenga la adición de las raíces elevado al cuadrado. Pero si por el contrario los términos presentan signos negativos y positivos, el paréntesis se establece con la sustracción de las raíces.

Si no entendiste el tema te invito a visitar el siguiente link:
Actividad 6:
Realizar Los siguientes ejercicios utilizando trinomio cuadrado perfecto:
4.2. Trinomio de la formo x2 + bx + c

Pueden factorizarse encontrando dos enteros, r y s, cuya suma sea b y cuya resta sea c. Reescribe el trinomio como x2 + rx + sx + c luego agrupa y aplica la propiedad distributiva para factorizar el polinomio.
Ejemplo1:
Este trinomio se puede representar geométricamente de la siguiente forma:

Si reorganizamos las figuras geométricas
obtenemos
Entonces podemos determinar el área de la fi gura de la siguiente manera:
4.2.1. Explicación algebraica:
Procedimientos:
Ejemplo1:
Paso1: Hallamos la raíz del cuadrado del término que cumpla con ser un cuadrado perfecto.
Paso2: Se construyen dos paréntesis cada uno con la raíz, obtenida en el paso anterior.
Paso 3: Buscamos dos términos que al ser multiplicados nos dé como resultado el término independiente y que al ser sumados o restados se obtenga el coeficiente del segundo término de la expresión algebraica.
En este caso necesitamos dos números que multiplicados nos den 45 y sumados nos den -18.
(-15) (-3) = 45
(-15) + (-3) = -18
Paso 4: Revisamos que los signos nos coincidan al realizar las suma o la resta y ubicamos los números en los paréntesis, acompañados de la raíz cuadrada obtenida, en el primer paso.


Si Quieres afianzar más sobre el tema, observa el siguiente video:
4.3. Trinomio de la formo ax2 + bx + c


Paso 3: Busco dos números que multiplicados me den 64 y restados me den 12.
(16) (-4) = -64
16 + (- 4) = 12
Por tanto, los paréntesis quedaran así: (4r + 16) (4r - 4)
Paso 4: Ya factorizamos el polinomio que se obtuvo al multiplicar toda la expresión por 4, pero en realidad el polinomio entregado inicialmente es 4r2 + 12r - 16, por tanto, debemos simplificar los paréntesis.
(4r + 16) (4r - 4), ambos paréntesis son posibles de simplificarlos por 1, 2 o 4, pero sólo se puede desarrollar la simplificación entre, exactamente, la cantidad por la cual fue multiplicada.
Entonces simplificaremos, los dos paréntesis por 2, puesto que al multiplicarlos obtenemos como resultado 4, cumpliendo con la condición, de ser exactamente la cantidad por la cual fue alterado el polinomio.

Obtenemos (2r + 8) (2r - 2), después de simplificar cada paréntesis. Otra forma de realizar esta simplificación es dividir por 4 sólo uno de los dos paréntesis. En tal caso, se obtendría:

Obtenemos (r + 4) (4r - 4), y aunque las dos expresiones son diferentes, si se multiplican los paréntesis entre ellos, se obtiene el polinomio entregado.
Nota: Lo que significa que un polinomio algebraico, es posible que sea factorizado de varias formas

Si quieres afianzar más sobre el tema, observa el siguiente video:
4.4. Factorización completando trinomios cuadrados perfectos por adición y sustracción

Cuando vamos a factorizar un trinomio que sea cuadrado perfecto, lo primero que realizamos es comprobar efectivamente que sea TCP.
¿Cómo se sabe que tenemos que factorizar por este método?
1. Verificamos si se puede sacar factor común. En este caso no le podemos sacar factor común ni a las variables ni a los números porque nueve no tiene factor común con 4 ni con 8
2. Verificar que esté ordenado el término. Acá ya está ordenado ya que los exponentes van disminuyendo tanto de izquierda a derecha como viceversa.
3. Verificamos que en los extremos se le pueda sacar raíz cuadrada, son cuadrados perfectos:
Si tienes dudas del ejercicio realizado, observa el siguiente video:

AUTOEVALUACION COMPONENTE HACER Y SER - CONVIVIR
(La realiza el estudiante)
