Grado 9 P3 - Geometría - Paralelas cortadas por secante, teoría de la demostración, semejanza, razón y proporción, segmentos

Rectas cortadas por paralelas
Recordemos: Para considerar los ángulos generados entre dos paralelas cortados por una secante, es necesario recordar el significado de rectas paralelas y recta secante.
Al trazar dos rectas en un mismo plano, estas rectas pueden ser:


Las rectas r y s son paralelas y la recta t es secante.
Dos rectas paralelas cortadas por una recta secante forman ocho ángulos, los cuales en la imagen están señalados por letras minúsculas: a, b, c, d, e, f, g, h
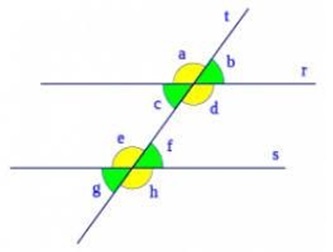
Estos, forman diferentes clases de ángulos, que se clasifican de acuerdo a las características que cumplan, de acuerdo a la posición que ocupen respecto a las rectas paralelas y a la recta secante.
Los ángulos formados entre dos rectas paralelas cortadas por una recta secante son:
1.Ángulos Colaterales 5. Ángulos Alternos Externos
Externos: (a,g)(b,h) (a,h)(b,g)
Internos: (c,e)(d,f)
2.Ángulos Internos 6. Ángulos Correspondientes
(c,d,e,f) (a,e)(b,f)(c,g)(d,h)
3.Ángulos Externos 7. Ángulos opuestos por el vértice.
(a,b,g,h) (a,d)(c,b)(e,h)(f,g)
4.Ángulos Alternos Internos
(c,f)(e,d)
TEORÍA DE LA DEMOSTRACIÓN

Glosario de términos antes de comenzar.
Hipótesis: Es una afirmación o conjetura acerca de una distribución de una o más variables aleatorias
Postulado: Proposición no evidente por sí misma ni demostrada, pero que se acepta, ya que no existe otro principio al que pueda ser referida.
Teorema: Es una proposición cuya verdad se demuestra.
Axioma: Un axioma es una frase matemática que todo el mundo admite como verdadera. Por lo tanto, se considera verdadera y no se tiene que demostrar que lo es. Los axiomas son las verdades elementales o verdades básicas.
Proposiciones: El término proposición es tomado de la lógica y suele ser definido como un enunciado que puede ser calificado de verdadero o falso. Se considera la proposición como un enunciado y este último como una frase u oración.
Premisas: En un argumento válido, las premisas implican la conclusión
QUE ENTENDEMOS POR DEMOSTRACIÓN

Esta palabra viene del latín «demonstratio» y significa lo mismo tal cual se entiende, su concepto etimológico es redundante. El concepto de demostración no es más que la verificación de una prueba anteriormente corroborada, sea verdadero o falso.
Por lo general, la demostración suele usarse para mostrar una prueba a terceras personas para disipar dudas o inducir la costumbre de que toda propiedad o teorema debe ser probada (aunque en la vida cotidiana la gente no acostumbra a comprobar lo que investiga, incluido en en las propias universidades.
Podemos decir que demostrar es volver a mostrar que un resultado sea verdadero o falso con los fundamentos adecuados. Un sinónimo de demostrar es comprobar, este último es lo mismo que decir que volver a probar. Los teoremas que demostramos en geometría son proposiciones condicionales o bicondicionales.
Por tanto, la demostración no es más que reafirmar una tesis de una hipótesis probada, punto. Es por ello que es inadecuado usar la palabra «prueba» en una demostración matemática de un teorema porque demostración y prueba son dos cosas distintas. Probar significa experimentar algo sin importar si la hipótesis es correcta o incorrecta, la demostración es solo verificar la tesis de la hipótesis anteriormente probada como verdadero o falso.
Aunque coloquialmente ya se aceptó como conceptos similares, su uso será a su criterio de cada quien, vayamos con el siguiente apartado.
DEMOSTRACIÓN MATEMÁTICA

La demostración en matemática es la reafirmación de los teoremas para asegurar la verdad los argumentos matemáticos anteriormente probados como verdaderos. Las premisas de un proceso de demostración de un consecuente que ya anteriormente ha sido probado pueden incluir definiciones, axiomas y/u otros teoremas.
Uno de los puntos fuertes de la demostración matemática es volver a reafirmar un teorema que anteriormente se probó su veracidad bajo una serie de procedimientos matemáticos también aceptados como verdaderas.
CONJETURA EN LAS MATEMÁTICAS
Tomemos al número 6, sus divisores son el 1, 2 y el 3, pero si sumamos estos divisores, nos da como resultado el número 6, este tipo de números se les llamó números perfectos.
Por definición, los números perfectos resulta ser igual a la suma de todos los divisores propios que esta posea. Euclides estudió estos resultados y encontró los primeros 4 primeros números perfectos que tenían una propiedad inusual. Encontró la siguiente formula por inducción básica que:
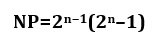
Donde NP significa números perfectos y el valor resultó ser
números primos. Esta generalidad lo supuso solo porque descubrió los cuatro
primeros números perfectos que cumplen esta propiedad, estos son:
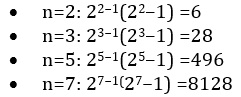

Pero los matemáticos de épocas antiguas dejaron por sentado que todos los números primos para NP tenían que ser números perfectos, esta afirmación sin demostración se le llama conjetura.
Existen otras conjeturas como son:
- La conjetura de Goldbach.
- La conjetura de los primos gemelos.
- La conjetura de Collartz
- Hipótesis de Riemann
- Conjetura de Beal
- Conjetura de Mertens
La mayoría de las conjeturas en matemática no han sido demostradas, considerándose como posibles afirmaciones y creencias especulativas hasta que pueda demostrar su veracidad o falsedad, pero también existen otras que lograron ser demostrados como verdaderos, por tanto, pasan a ser reformuladas como teoremas
VIDEOS:
Demostración matemática: https://www.youtube.com/watch?v=8GTKfo1W6_A
Conjeturas matemáticas sin resolver: https://www.youtube.com/watch?v=d2CHQy7-Ccs
Actividad1
En grupos de 2, escoger una de las conjeturas y exponerla utilizando la herramienta Power Point, Prezi o Sway.
EL LENGUAJE DE LA DEMOSTRACIÓN

No se puede evitar el lenguaje informal en la formalización estrictas de las matemáticas, no existe una formalización completa y pura sin usar palabras cotidianas o por lo menos palabras con propiedad con cierto grado de rigor.
Existen otros conceptos que no se pueden definir con precisión, por ejemplo, la palabra «conjunto», este puede significar una colección de objetos (sea objetos virtuales o reales), sin embargo, la palabra «colección» y «conjunto» son sinónimos. También existen en el lenguaje coloquial palabras indefinibles como ¿qué es el color azul?, o ¿qué es bonito? sin usar dentro de su concepto la palabra «feo» y ninguno de sus contrarios, etc.
De la misma manera ocurre con el lenguaje de las demostraciones matemáticas, por más formal que sea, siempre requerida de algún lenguaje informal. Este es un tema un poquito extenso para otra entrada en una sección distinta.
En resumen, las demostraciones matemáticas le conciernen la estructura de los lenguajes formales para no caer en ambigüedades, este tipo de lenguajes se les llama fórmulas bien formadas, muy usado y constantemente reformulados hasta lograr una demostración matemática óptima, rigurosa y fuera de toda contradicción.
PROPOSICIONES
El término proposición es tomado de la lógica y suele ser definido
como un enunciado que puede ser calificado de verdadero o falso. Se considera la proposición como un enunciado y este
último como una
frase u oración.

PROPOSICIONES CONDICIONALES
Si se conectan dos enunciados colocando la palabra
"si" antes de la condición - llamada antecedente - y
después de la palabra "entonces", el consecuente; la
proposición compuesta resultante se llama un condicional, proposición
hipotética o implicación.
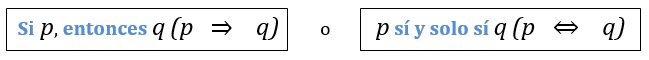
Donde P es la hipótesis del teorema y q es la tesis o conclusión. Para demostrar un teorema se aplica uno de los siguientes métodos de razonamiento: Método directo o método indirecto.
El proceso de demostración es un desarrollo creativo, en el que se enlazan (por medio de argumentaciones lógicas) definiciones, postulados y teoremas ya demostrados, para llegar a una conclusión.

CONDICIÓN SUFICIENTE

CONDICIÓN NECESARIA

Con base a estos resultados, deducimos que la conclusión es condición necesaria para las premisas y las premisas es condición suficiente para la conclusión.
COMBINACIÓN DE LAS CONDICIONES SUFICIENTES Y NECESARIAS
Pero la cosa cambia cuando agregamos un requisito más para el segundo caso anterior (para el caso de la condición necesaria), donde:
p: a y b son números pares.
q: a+b es par.
s: a⋅b es par.

a+b=par⋯(I)
a⋅b=par⋯(II)
De (I) despejamos a y reemplazamos en (II), tenemos:
a(par-a)=par⋯(III)
Si a es impar la condición (III) no se cumple, pero si a es par, esta misma condición se cumple tranquilamente, como a=par, lo reemplazamos en (I), obtenemos:
par+b=par
Para que esta última fórmula se cumple, es obligando que b sea también par. Por tanto, concluimos que las proposiciones q y s no solo son condiciones necesarias, sino también son condiciones suficientes para que p se cumpla.

Espero que con estos ejemplos quede claro cuando debe decirse que un argumento es condición suficiente, condición necesaria y cuando es una condición suficiente y necesaria a la vez. Estas palabras son muy usadas en matemáticas para diferenciar muchos casos demostrativos.

Por fin, comencemos con los diferentes métodos de demostraciones matemáticas que estábamos ya esperando desde un inicio.
VIDEOS:
Lógica proposicional: https://www.youtube.com/watch?v=vKe0UKSpNQQ
Condición suficiente Vs condición necesaria: https://www.youtube.com/watch?v=CWKuN_VqxmY
Si quieres ahondar más sobre el tema de condiciones necesarias y suficientes, te comparto este archivo:
METODOS DE DEMOSTRACIÓN
Los métodos que trataremos a continuación son los más habituales en el área de matemáticas y las más usadas, naturalmente la que vendrá en breve es la más usada de todas y si se me permite la palabra aquí, también la más confiable porque pueden observar todo el proceso de la demostración sin hacer supuestos.
El resto de los métodos son usados cuando no es posible usar métodos directos, esto dependerá de cómo y de qué manera se anuncie una proposición matemática, comencemos con el primero método.
1· MÉTODO DIRECTO
Pasos para una demostración por el método directo
1. Se determina claramente la hipótesis o la tesis del teorema que se va a demostrar. Se reformula el teorema en términos de una proposición condicional. p→q
2. Se realiza una construcción geométrica a partir de la hipótesis y la tesis, en estas se incluyen las construcciones auxiliares que apoyen la demostración del teorema. Se asume que p es una condición dada como cierta. Generalmente conviene hacer un dibujo que ilustre lo dado.
3. Se relaciona la hipótesis con las definiciones, postulados y teoremas demostrados anteriormente, para establecer una sucesión lógica de proposiciones que permitan comprobar la validez de la tesis. Generalmente este paso de la demostración se presenta en dos columnas.
a. En la primera se escriben las proposiciones verdaderas que permiten comprobar la validez de la tesis.
b. Se escribe la justificación correspondiente.
4. Se afirma lo demostrado
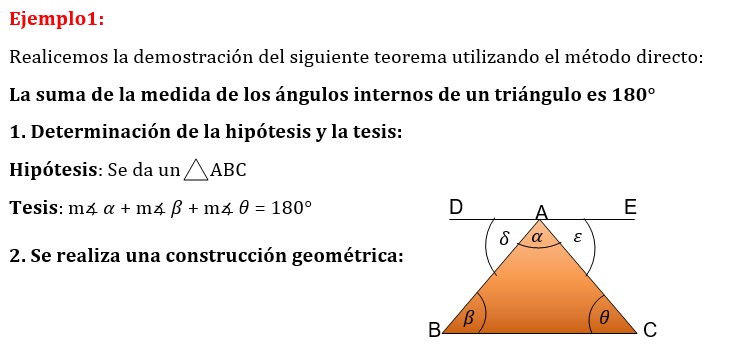
Para
este teorema se construye un triángulo con vértices ABC, y se traza una recta
DE que pasa por A y que sea paralela al lado BC
3. Se escriben las proposiciones que permiten probar la validez de la tesis con sus respectivas funciones.
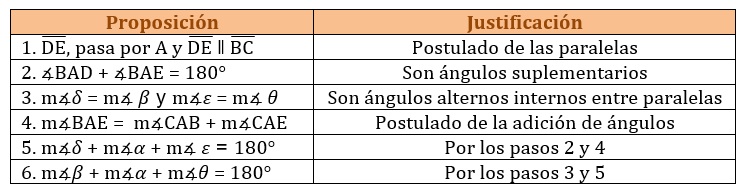

2· MÉTODO INDIRECTO
Los principales métodos indirectos de demostración son la contrarrecíproca y la reducción al absurdo.





Te invito a observar los siguientes videos para afianzar más los temas sobre métodos de demostración:
Directa: https://www.youtube.com/watch?v=HGKyLuoXZEg&t=499s
Directo, Indirecta, absurdo: https://www.youtube.com/watch?v=yAGoR6FUyi8
Contra recíproco: https://www.youtube.com/watch?v=C355XcNC7qA
Contra Posición: https://www.youtube.com/watch?v=Y9i7bMrLM_U
Si quieres leer más sobre el tema te invito a que visites el siguiente link:
https://es.quora.com/Cu%C3%A1l-es-un-ejemplo-simple-de-demostraci%C3%B3n-por-contradicci%C3%B3n
2. SEMEJANZA DE TRIÁNGULOS
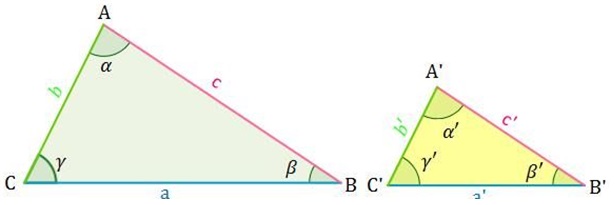
La semejanza de triángulos es una característica que hace que dos o más triángulos sean semejantes.
Dos triángulos son semejantes cuando tienen sus ángulos iguales (o congruentes) y sus lados correspondientes (u homólogos) son proporcionales.
Son lados homólogos los opuestos a ángulos iguales.
Aquí tenemos un caso, donde se ven los elementos homólogos (ángulos y lados) con la igualdad o congruencia de sus ángulos y la proporcionalidad de los lados (Ver Gráfico anterior)
En los triángulos semejantes se cumplen las condiciones siguientes:
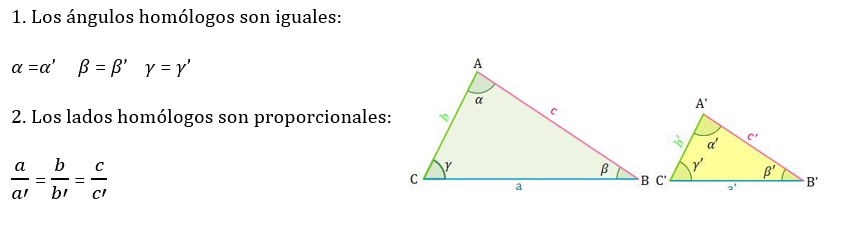
3· RAZÓN DE PROPORCIONALIDAD
A r se le denomina razón de semejanza o de proporcionalidad.
Se cumple que la razón de los perímetros de dos triángulos semejantes es también la razón de semejanza y que la razón de sus áreas es el cuadrado de la razón de semejanza:
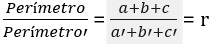
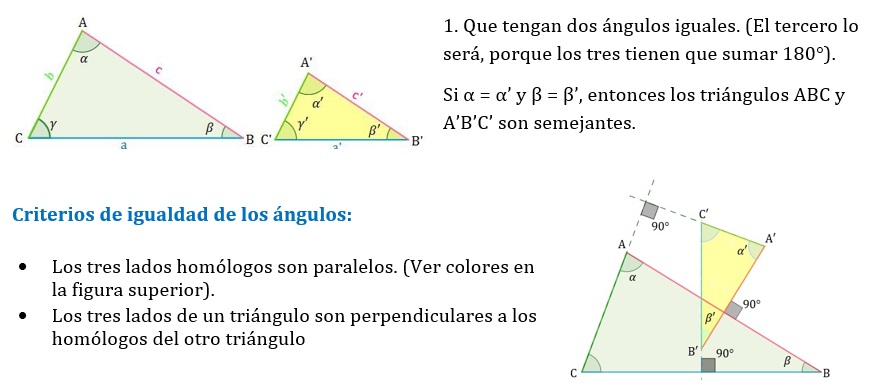
Para saber si dos triángulos son semejantes no es necesario conocer sus tres ángulos y sus tres lados. Existen tres criterios para asegurarlo.
Criterios de semejanza de dos triángulos
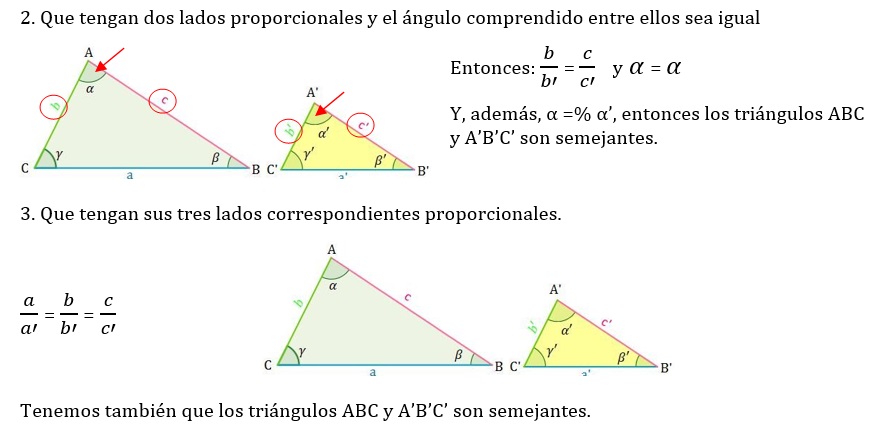
4· TRIÁNGULOS EN POSICIÓN DE TALES
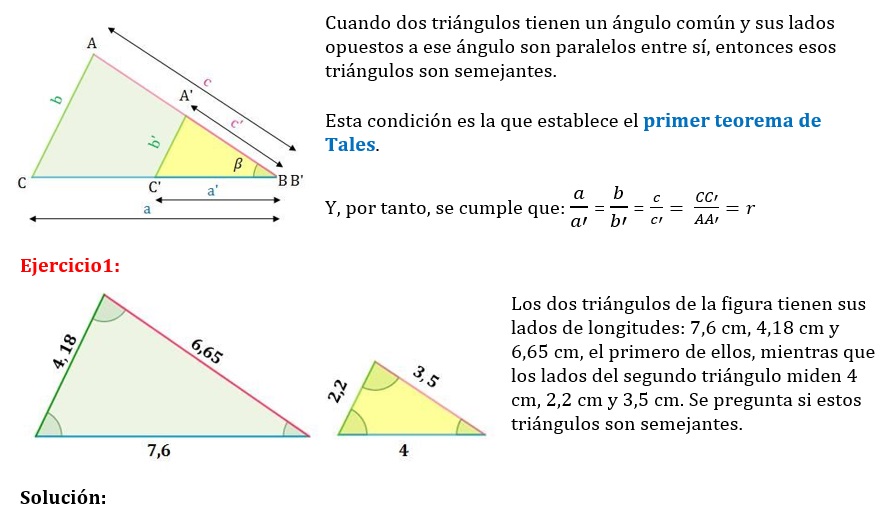


VIDEO:
Te invito a observar el siguiente video de triángulos semejantes y proporcionales:
https://www.youtube.com/watch?v=Pgb3H4Su1EY&t=35s
Teorema del coseno:
https://www.youtube.com/watch?v=Y285KwXAuuY
ACTIVIDAD2:
1. Los catetos de un triángulo rectángulo que miden 24 m y 10 m. ¿Cuánto medirán los catetos de un triángulo semejante al primero cuya hipotenusa mide 52 m?
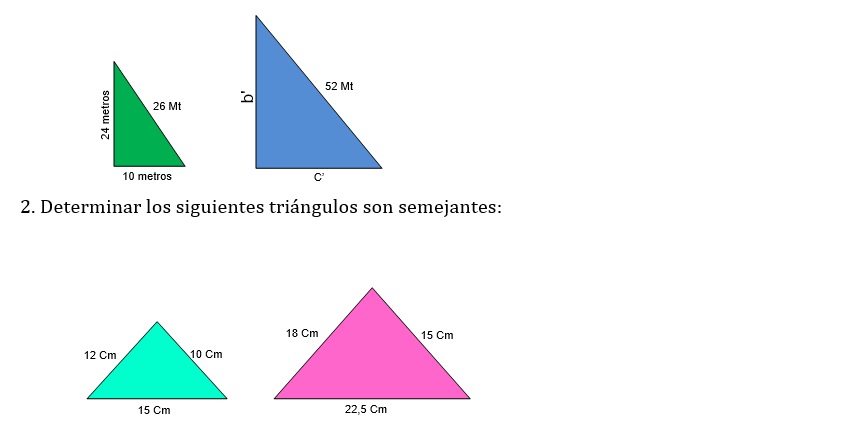
5· PROPORCIONALIDAD DE SEGMENTOS
5.1. Razón entre dos segmentos:

Si calculamos la razón de dos segmentos, conociendo la medida de cada uno de ellos con respecto a un segmento unidad, el resultado es siempre el mismo independiente de la unidad de medida elegida, aunque ha de ser siempre la misma para medir ambos segmentos.
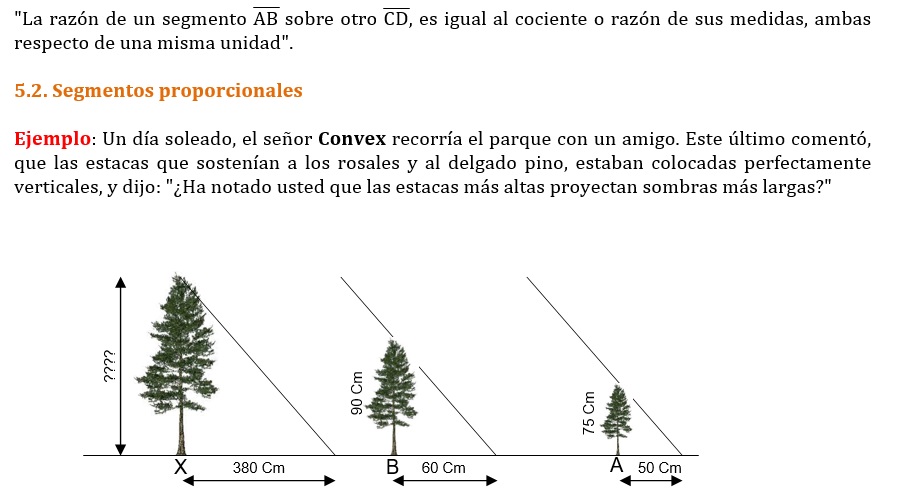
Es cierto - respondió Convex, además, las sombras son proporcionales a las alturas; por eso, con ayuda de una estaca podría hallar la altura del pino sin medirlo.
Amigo (sorprendido) ¿Qué quieres decir con todo eso?
Convex Pues Mide las alturas de las estacas y las sombras de éstas, y del pino
Amigo. He aquí las medidas:

Si quieres observar la razón entre dos segmentos te invito a experimentar en Geogebra:
https://www.geogebra.org/m/wxAsJrsP
ACTIVIDAD3:
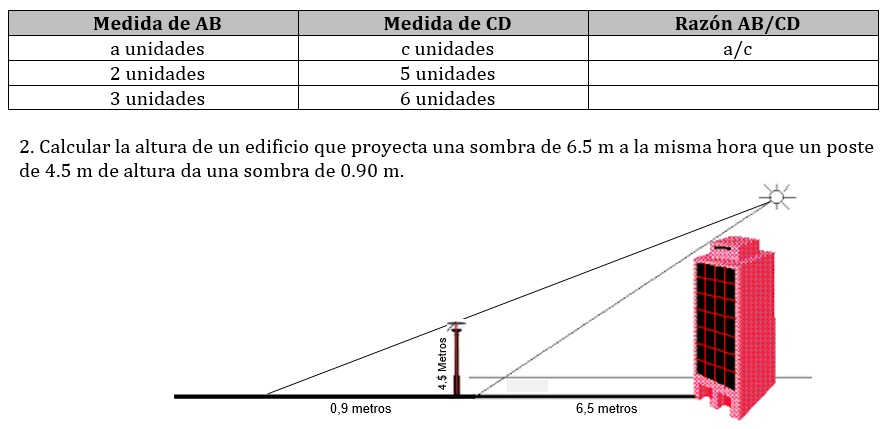
1. En este ejercicio tienes que calcular la razón de los segmentos AB y CD, en los siguientes casos:
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%): a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%): a. Prueba Bimestral
• Ser - Convivir (25%): a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
1. Nunca (1.0) 2. Casi Nunca (2.0) 3. A veces (3.0) 4.Casi Siempre (4.0) 5. Siempre (5.0)
AUTOEVALUACION COMPONENTE HACER Y SER - CONVIVIR
(La realiza el estudiante)
Acá puedes descargar la guía:
RECUPERACIÓN 3ER PERIODO
Aquí encontraras el examen de recuperación del tercer periodo sobre el tema de rectas paralelas cortadas por una secante. Realiza los ejercicios en una hoja marcada y entregala al docente para su revisión, al entregarla el profesor te hará una pregunta para verificar si tu hiciste el trabajo o es una copia de un compañero.
