Grado 9 P3 - Estadística- Demostración, semejanza, razón y proporción

RECORDEMOS:
El factorial de un número entero positivo n, o el factorial de n, o n factorial, que se simboliza n!, se define en principio como el producto de todos los números enteros positivos desde 1 ( es decir, los números naturales) hasta n.
La forma de definir el factorial es la siguiente:
0! = 1
1! = 1
2! = 1 · 2
3! = 1 · 2 · 3...
n! = 1 · 2 · 3 · . . . · n = n · (n − 1)!
✶ Su utilidad estriba en que se utiliza en la mayoría de las fórmulas de la COMBINATORIA
1. PROBABILIDAD FRECUENCIAL

1.1. Experimentos aleatorios:
Un experimento aleatorio es cualquier situación que se puede repetir indefinidamente bajo las mismas condiciones, pero de la que se desconoce cúal será su resultado. Por el contrario, cuando el resultado es predecible, se denomina experimento determinista.
Si el resultado se repite gran número de veces entonces aparece algún modelo de regularidad estadístico en los resultados obtenidos, de tal forma que se puede prever el resultado sin necesidad de volver a realizar el experimento.
1.2. Espacio Muestral (E,S,Ω o U)
Consiste en un conjunto de todos los posibles resultados individuales de un experimento aleatorio.
Ejemplo1:
Para el experimento aleatorio de lanzar un dado, hay 6 posibilidades, resultados que corresponden al número de puntos que hay en cada cara. Así, el espacio muestral para ese experimetno es el conjunto Ω = {1,2,3,4,5,6}
1.3. Evento o suceso
Conjunto de uno o más resultados del experimento aleatorio.
Si A = {obtener un número 5 al lanzar un dado}, entonces, A={5}.
Si B = {obtener un número mayor que 3 al lanzar un dado}, entonces, B={4, 5, 6}.
Si C = {obtener un número par al lanzar un dado}, entonces, C={2, 4, 6}.
Si D = {obtener al menos 1 gato al lanzar 2 monedas}, entonces, D={(P, G), (G, P), (G, G)}
1.4. Regla de Laplace:
La probabilidad frecuencial es una medida obtrenida de la experiencia de algún fenómeno o experimento aleatorio que permite estimar a futuro un comportamiento; sin embargo, no es definitrva, por lo que es importante saber interpretar los resultados que se obtienen.
La probabilidad frecuencial de un evento A, que se denota P(A) y se conoce como Regla de Laplace, se obtiene dividiendo el número de veces que ocurre el evento entre el número total de veces que se realizó el experimento.


Video:
Si se te dificulta el tema, te invito a observar el siguiente video:
Ejercicios interactivos:
Realizar ejercicios interactivos sobre la regla de Laplace, al terminar debe ser presentado al docente.
Actividad1:

1. Ten en cuenta el experimento aleatorio "Sacar una carta al azar de una baraja española". Luego, halla la probaibilidad de cada suceso.
a. Salir un caballo
b. Salir un oro
c. Salilr un número menor que seis
d. Salir un número mayor que seis
2. Halla las probabilidades que se indican en la siguiente situación.
En un intercambio cultural participan 17 estudiantes colombianos, 8 brasileros, 4 argentinos y 2 holandeses. Entre los participantes se elige uno al azar.
a. Cual es la probailidad de que sea colombiano?
b. Cual es la probabilidad de que sea brasilero?
3. Copia en tu cuaderno la tabla siguiente, en la que se muestra la distribución de tres cursos de un colegio y complétala:

Se Escoge un estudiante al azar
a. Cual es la probabilidad de que pertenezca a 901?
b. Cual es la probabilidad de que sea niña?
c. Cual es la probabilidad de que sea niña y que esté en 902?
d. Cual es la probabilidad de que sea niña y que esté en 903?
e. Cual es la probabilidad de que sea niño y que esté en 901?
2. TÉCNICAS DE CONTEO

En el grado octavo vimos las técnicas de Diagrama de árbol, principio multiplicativo y principio aditivo, en esta oportunidad veremos 2 técnicas muy importantes que son las combinaciones y las permutaciones.
2.1. PERMUTACIONES:
Permutar es colocar elementos en distintas posiciones.
También, se llama permutaciones de «n» elementos en «r» posiciones a las distintas formas en que pueden ordenarse los «n» elementos ocupando únicamente las «r» posiciones. Siempre y cuando n ≥ r.
Hay que tener en cuenta lo siguiente:
- Sí importa el orden, ya que el intercambio entre dos elementos distintos genera una nueva permutación.
- No se repiten los elementos, ya que de repetirse o ser iguales entre si, al intercambiarlos no se genera una nueva permutación.
Para obtener el total de maneras en que se pueden colocar «n» elementos en «r» posiciones se utiliza la siguiente fórmula:

Observación.
Si en dado caso, n = r ; para calcular el total de permutaciones se utiliza la siguiente fórmula:

Ejemplo1:
Eduardo, Carlos y Sergio se han presentado a un concurso de pintura. El concurso otorga $2.000.000 al primer lugar y $1.000.000 al segundo. ¿De cuántas formas se pueden repartir los premios de primer y segundo lugar?
Solución:
En este caso, si importa el orden, ya que no es lo mismo quedar en primer lugar que en segundo, además, los premios son diferentes.
Por ejemplo, un arreglo
o disposición, es que Carlos ocupe el primer lugar y Sergio el
segundo. Otro arreglo, sería que Sergio ocupe el primer lugar y Eduardo
el segundo. El número total de arreglos o formas lo calculamos con la fórmula:

Ejemplo2:
Obtener el número de permutaciones de las cinco letra a, b, c, d, e tomadas de tres en tres.
Solución:
La fórmula a usar es

Ejemplo3:
De cuántas maneras pueden sentarse cinco alumnos en un salón de clase que tiene ocho bancos individuales.
Solución:
Usamos la fórmula

VIDEO:
Si se te dificultó el tema de permutaciones, te invito a observar el siguiente video.
Ejercicios Interactivos:
Realizar los siguientes ejercicios interactivos sobre permutaciones. Al terminar tómale el pantallazo a tus resultados y envíalo al grupo de WP, o en su defecto enséñale los resultados al docente.
https://www.neurochispas.com/practica-algebra/permutaciones/
Actividad2:
Los estudiantes presentarán resueltos los siguientes ejercicios
1. Halla el valor de cada expresión:
1. P(15,3) 2. P(5,3) + P(7,3) 3. P(6,4) . P(4,2)
4. P5 5. P(8,2) - P3 6. P(9,2)/P4
Pregunta 2.
a) ¿De cuántas formas distintas se pueden ordenar las letras de la palabra JUAN?
b) ¿Cuántas ordenaciones distintas empezarán por vocal?
Pregunta 3.
Cuatro libros de matemáticas, tres de física y dos de química han de ser colocados en una estantería
a) ¿Cuántas colocaciones distintas se pueden lograr si los libros de cada materia han de estar juntos?
Pregunta 4.
¿De cuántas formas pueden colocarse los 11 jugadores de un equipo de fútbol teniendo en cuenta que el portero no puede ocupar otra posición distinta que la portería?
Pregunta 5.
Se tienen 15 bolas numeradas y se desea conocer
a) ¿Cuántos grupos distintos de 3 bolas se pueden construir con las 15 bolas numerada
Si se te dificultó el tema de permutaciones, te invito a observar el siguiente video.
https://www.youtube.com/watch?v=3svszuOz368
2.2. COMBINACIONES:
Una combinaciones es un conjunto o colección de objetos en un orden no especificado, no se repiten.
- El número de combinaciones de «n» objetos de «r» en «r» se asocia con el número de subconjuntos de r elementos que tiene un conjunto de n elementos.
- Las combinaciones son muy parecidas a las permutaciones, con la diferencia en que en los conjuntos que se forman si importa el orden de manera que: abc = ab, ac, bc
Ejemplo 1.
Si A = {a, b, c, d}
¿Cuántas combinaciones de dos letras se pueden obtener?
Esto equivale a preguntarse ¿Cuántos subconjuntos de dos elementos tiene el conjunto A?
Solución:
La respuesta es: {a, b} ,{a, c} , {a, d} ,{b, c} , {b, d} ,{c, d}
Seis es el número de combinaciones de dos letras que podemos conseguir con las cuatro letras dadas.
Para indicar el número
de combinaciones de «n» objetos tomados de r se usa la fórmula:

Ejemplo 2.
Consideremos de nuevo el conjunto: A = {a, b, c, d}
Veamos entonces la diferencia, formando permutaciones y combinaciones de tres elementos.

Observación.
La diferencia entre una permutación y una combinación es que en la permutación el interés se centra en contar todas las posibles selecciones y todos los posibles arreglos entre éstas, mientras la combinación el interés es contar las selecciones diferentes. Por cada combinación hay r! permutaciones.
Ejemplo 3.
¿Cuántas ternas para candidatura de director pueden formarse de un grupo de 15 maestros?
Solución.
Se pide el número de combinaciones de 15 elementos tomados de tres en tres.
Usamos la fórmula

Ejemplo 4
Javier, Gonzalo, Manuel, Pamela y Paola se han postulado a la directiva de su curso, pero solo 3 de ellos pueden quedar, ¿cuántas directivas posibles hay?.
Solución.
En éste caso se trata de formar combinaciones entre los postulantes, pues si por ejemplo se elije a Javier, Gonzalo y Paola es lo mismo que se elija a Paola, Gonzalo y a Javier, lo que corresponde a una combinación de 3 elementos de un total de 5, por lo tanto:

Ejemplo 5
En una clase de 10 alumnos van a distribuirse 3 premios. Averiguar de cuántos modos puede hacerse si:
1. Los premios son diferentes.
2. Los premios son iguales.
Solución.
Si suponemos una misma persona NO puede recibir más de un premio, luego los alumnos NO se pueden repetir:
Caso 1.
Los premios son diferentes (no es lo mismo ganar el primer premio que el segundo) importa el orden,entonces se trata de una permutación donde:

Caso 2.
Si los premios son iguales, no importa el orden, son indistinguibles. Se trata de una combinación

Ejemplo 6
Un chef va a preparar una ensalada de verduras con tomate, zanahoria, papa y brócoli. ¿De cuántas formas se puede preparar la ensalada usando solo 2 ingredientes?
Solución.
En este caso, no importa el orden en que se tomen los ingredientes para la ensalada, pues da igual si es una ensalada de tomate con zanahoria, que una ensalada de zanahoria con tomate, ya que al final, el chef mezclará los dos ingredientes.
Un arreglo podría ser zanahoria y tomate, otro arreglo podría ser tomate y papa, otro arreglo podría ser papa y brócoli. El problema nos indica que solo se pueden usar 2 ingredientes en la ensalada. El número total de arreglos o formas lo calculamos con la fórmula:
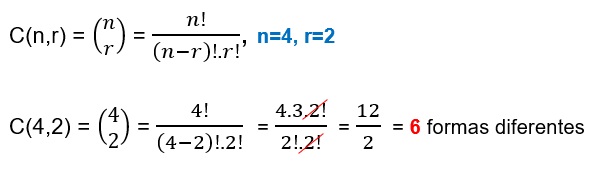
Ejemplo 6
Se va a programar un torneo de ajedrez para los 10 integrantes de un club. ¿Cuántos partidos se deben programar si cada integrante jugará con cada uno de los demás sin partidos de revancha?
Solución.
En este torneo se van a realizar partidas de ajedrez en cada una de las cuales participan 2 jugadores. Por ello, necesitamos ordenamientos de 2 en 2, es decir, r = 2. Además, en estos ordenamientos participarán los 10 jugadores, por eso, n = 10.
En este caso, no importa
el orden, ya que solo necesitamos agrupar los jugadores, es igual que juegue
Jorge contra Carlos, que Carlos contra Jorge. Además, no hay partido de
revancha, es una sola partida con cada contrincante

Video:
Si se te dificultó el tema de combinaciones, te invito a observar el siguiente video.
Ejercicios Interactivos:
Realizar los siguientes ejercicios interactivos sobre combinaciones. Al terminar tómales el pantallazo a tus resultados y envíalo al grupo de WP, o en su defecto enséñale los resultados al docente.
https://www.neurochispas.com/practica-algebra/combinaciones/
Actividad3:
Los estudiantes presentarán resueltos los siguientes ejercicios
Pregunta 1. Halla el valor de cada expresión:
1. C(15, 3) 2. C5 3. C(5, 3) + C(7, 3)
4. C(8, 2) − C3 5. C(6, 4) · C(4, 2) 6. C(9, 2)/C4
Pregunta 2.
¿De cuántas formas pueden mezclarse los siete colores del arco iris tomándolos de tres en tres?
Pregunta 3.
A una reunión asisten 10 personas y se intercambian saludos entre todos.
¿Cuántos saludos se han intercambiado?
Pregunta 4.
a) ¿Cuántas diagonales tiene un pentágono?
b) ¿Cuántos triángulos se pueden formar con sus vértices?
Pregunta 5.
Una persona tiene cinco monedas de distintos valores.
¿Cuántas sumas diferentes de dinero puede formar con las cinco monedas?
3. PRINCIPIOS DE MULTIPLICACIÓN

El principio de multiplicación permite encontrar el número de elementos del espacio muestral en aquellos experimentos aleatorios en los cuales el orden es relevante y puede haber repetición.
Definición:
Dado un experimento aleatorio con una población de N elementos y una muestra de n elementos, el número de formas distintas de resultar el experimento es:

Donde #(S) corresponde al número de elementos del espacio muestral
Ejemplo1:
Si se desea hacer una rifa en la que cada boleta tiene un número de tres cifras, ¿cuántas boletas se deben imprimir?
Solución:
En este caso como cada cifra tiene diez posibilidades (0, 1, 2, 3, ..., 9), N=10, y como el número debe tener tres cifras, entonces n=3. Luego,

Por lo tanto, se deben imprimir 1000 boletas distintas.
El principio de multiplicación también se aplica para casos en los cuales se debe obtener una muestra considerando poblaciones diferentes o casos en los cuales es posible determinar las etapas necesarias para realizar un experimento aleatorio.
Ejemplo2:
En una determinada fábrica, para que un mueble llegue a su ensamble final, necesita pasar por tres secciones:
Sección 1: Carpintería
Sección 2: Pintura
Sección 3: Tapizado
En la sección de carpintería hay tres operarios, en la sección de pintura hay dos operarios, y en la sección de tapizado hay cuatro operarios. En cada sección, el operario correspondiente se encarga de trabajar específicamente en ese mueble. ¿De cuántas formas se puede ensamblar un mueble?
Solución:
La situación se puede representar de la siguiente forma




Ejemplo4:
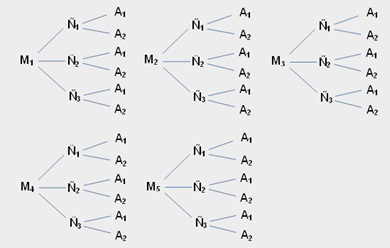
Un almacén agropecuario ofrece a sus clientes 5 tipos de semillas de maíz, 3 tipos de semillas de ñame y 2 tipos de semillas de arroz. Si un campesino va a comprar un tipo de semilla de cada producto, ¿cuántas opciones tiene para escoger los tres tipos de semilla?
Solución:
La situación se puede representar de la siguiente forma:


VIDEO
Observa el siguiente video para afianzar el concepto de principios de la multiplicación:
PRACTICA:
Desarrolla los ejercicios jugando en el siguiente link:
https://es.educaplay.com/recursos-educativos/6683755-principio_de_la_multiplicacion.html
Actividad5:
1. Una sala de lectura tiene 5 puertas:
a) ¿de cuántas maneras puede entrar a la sala un estudiante y salir por una puerta diferente?
b) ¿y si sale por cualquier puerta?
2. De la ciudad A a la ciudad B, se puede ir mediante 2 buses o 3 trenes. De la ciudad B a la ciudad C se puede ir mediante 2 barcos, 2 trenes o 3 aviones. ¿De cuántas formas se puede ir de la ciudad A a la ciudad C, pasando por B?
3. ¿Cuántos números de dos cifras pueden formarse con los dígitos: 1; 2; 3; 4 y 5, si:
a) Si se pueden repetir los dígitos.
b) No se pueden repetir los dígitos.
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%): a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%): a. Prueba Bimestral
• Ser - Convivir (25%): a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
1. Nunca (1.0) 2. Casi Nunca (2.0) 3. A veces (3.0) 4.Casi Siempre (4.0) 5. Siempre (5.0)
AUTOEVALUACION COMPONENTE HACER Y SER - CONVIVIR
(La realiza el estudiante)
