
Grado 9 P3 - Matemáticas - Potenciación, Radicación de Números Reales

RECORDEMOS
Una multiplicación formada por factores
iguales se puede escribir en forma de potencia:

donde a, conocida como la base, es el número que se repite y b, conocido como el exponente, es el número de veces que se repite el factor.
Por ejemplo, tendríamos que

Para este ejemplo de potencia tendríamos que la base es 6, mientras que el exponente es 5.
1. POTENCIA DE NÚMEROS RACIONALES

1.1. POTENCIAS CON EXPONENTES ENTEROS
A. Potencia con exponente entero positivo

B. Potencia con exponente entero negativo
Una potencia con exponente negativo es igual al inverso multiplicativo de la base de la potencia elevado al exponente positivo (siempre que la base sea distinta de cero).
Así, tenemos que:

1.2. POTENCIAS DE NÚMEROS RACIONALES
A. Potencia de número positivo
Cuando en una potencia la base es fraccionaria, elevamos tanto el numerador como el denominador al exponente.

B. Potencia con base fraccionaria y exponente negativo
Una potencia con base fraccionaria y exponente negativo es igual al inverso multiplicativo del base elevado al exponente positivo. Recordemos que el inverso de una fracción es igual a cambiar el numerador y el denominador entre sí, esto es, el inverso

1.3. POTENCIA CON EXPONENTE RACIONAL O FRACCIONARIO
Una potencia con exponente fraccionario es igual a una raíz cuyo índice es el denominador de la fracción y el exponente del radicando es el numerador
A. Potencia de
exponente racional positivo

B. Potencia de exponente racional negativo
Al igual que en los casos anteriores, cuando el exponente es fraccionario negativo, es equivalente a elevar el inverso multiplicativo de la base al exponente positivo. Así, tendríamos que
1.4. APLICACIÓN DE LAS PROPIEDADES DE POTENCIACIÓN
Ejemplos:
1. Determinar el valor de cada potencia aplicando las propiedades de la potenciación:

2. Simplificar las siguientes expresiones algebraicas:

Actividad1:
TODAS LAS RESPUESTAS DE LOS EJERCICIOS DEBEN JUSTIFICARSE CON LAS RESPECTIVAS OPERACIONES, PROCEDIMIENTOS O PROCESOS.
1. Resuelve aplicando las propiedades de las potencias:
Video:
Si no te quedó claro el concepto, te invito a que observes estos videos:
https://www.youtube.com/watch?v=c6uUumHcj18
O este otro:
Actividad 2.
Desarrollar la siguiente actividad interactiva: (Contestarla y enviar el pantallazo del resultado vía wp)
2. OPERACIONES CON NÚMEROS EN NOTACIÓN CIENTÍFICA.
Cuando trabajan con números muy grandes o muy pequeños, los científicos, matemáticos, e ingenieros normalmente usan la notación científica para expresar dichas cantidades. La notación científica usa la notación exponencial. Los siguientes ejemplos muestran la notación científica.
Año luz: El número de millas que viaja la luz en el transcurso de un año, alrededor de 5,880,000,000,000

Átomo de Hidrógeno: tiene un diámetro de alrededor de 0.00000005
mm

El cálculo de números muy grandes es más fácil si usamos la notación
científica.
Cuando un número se escribe en notación científica, el exponente te dice si el término es un número muy grande o muy pequeño. Un exponente positivo indica un número grande y un exponente negativo indica un número muy pequeño que está entre 0 y 1.
Como es tan útil, veamos más a detalle el formato de la notación científica

Observa los números siguientes. ¿Cuál de los números está escrito en notación científica?

Escribiendo Notación Decimal en Notación Científica
Ahora comparemos algunos ejemplos de números expresados en notación científica y en notación decimal estándar para entender cómo se convierte de uno al otro. Observa las tablas siguientes, Pon atención al exponente en la notación científica y la posición del punto decimal en la notación decimal.

Para escribir un número grande en notación científica, movemos el punto decimal a la izquierda hasta obtener un número entre 1 y 10. Como mover el punto decimal cambia el valor, es necesario multiplicar el decimal por una potencia de 10 para que la expresión conserve su valor.
Ejemplo:

Observa que el punto decimal fue movido 5 lugares hacia la izquierda, y el exponente es 5.
Para escribir un número pequeño (entre 0 y 1) en notación científica, debes mover el punto decimal hacia la derecha y el exponente debe ser negativo.
Ejemplo:

Podrías notar que el punto decimal fue movido cinco lugares hacia la derecha hasta que obtuviste el número 4, que está entre 1 y 10. El exponente es −5.
Escribiendo Notación Científica en Notación Decimal
También puedes escribir notación científica como notación decimal. Por ejemplo, el número de millas que viaja la luz en un año es 5,88 x 10(12), y el átomo de Hidrógeno tiene un diámetro de 5 x10(-8) mm. Para escribir estos números en notación decimal, mueves el punto decimal el mismo número de lugares que el exponente. Si el exponente es positivo, mueves el punto decimal a la derecha. Si el exponente es negativo, mueves el punto decimal a la izquierda.

Por cada potencia de 10, mueves el punto decimal un lugar. Ten cuidado aquí y no te dejes llevar con los ceros - el número de ceros después del punto decimal siempre será 1 menos que el exponente porque se necesita una potencia de 10 para mover ese primer número a la izquierda del decimal.
Multiplicando y Dividiendo Números Expresados en Notación Científica
Los números escritos en notación científica pueden ser multiplicados y divididos de manera simple tomando ventaja de las propiedades de los números y de las reglas de los exponentes. Para multiplicar números en notación científica, primero multiplica los números que no son potencias de 10 (la a en a x 10(n)). Luego multiplica las potencias de diez sumandos los exponentes.
Esto producirá un nuevo número por una potencia de 10 distinta. Todo lo que tienes que hacer es comprobar que este nuevo valor esté en notación científica. Si no lo está, lo conviertes.

Para dividir números en notación científica, una vez más puedes aplicar las propiedades de los números y las reglas de los exponentes. Empiezas dividiendo los números que no son potencias de 10 (la a en a x 10(n)). Luego divide las potencias de diez restando los exponentes.
Esto producirá un nuevo número por una potencia de 10 distinta. Todo lo que tienes que hacer es comprobar que este nuevo valor esté en notación científica. Si no lo está, lo conviertes.

Nota: Observa que cuando divides términos exponenciales, restas el exponente en el denominador del exponente en el numerador.
Videos:
Si no te quedó claro el tema te invito a observar los siguientes videos:
y estos otros de notación científica (suma y resta):
Multiplicación:
Actividad 3.
1. Escribe en notación científica el número indicado en cada enunciado:
a. Un año luz es la distancia que recorre la luz en un año y equivales aproximadamente a
5 900 000 000 000 millas
b. El diámetro de un electrón mide aproximadamente 0,0000000000004 Centímetros
c. La masa de una molécula de oxígeno pesa aproximadamente 0,000000000000000000000053 gramos.
2. Escribe la notación científica de las siguientes cantidades:
a. 58 934 000 000 b. 0,00026
c. 97 000 000 000 d. 396 000 000 000
e. 0,0419 f. 215 000
g. 0,000000000325 h. 921 560 000 000
i. 0,0000000659 j.
634 000 000

4. Efectúa las siguientes operaciones aplicando notación científica y escribe su resultado en notación decimal:


6. Desarrollar los ejercicios interactivos: https://es.liveworksheets.com/worksheets/es/matem%C3%A1ticas/Potencias/Notaci%C3%B3n_cient%C3%ADfica_hf333263cx, Debe tomarse un pantallazo de la respuesta y enviarla al docente.
3· RADICACIÓN

La radicación es una de las operaciones inversas de la potenciación, que nos permite conocer la base de la potencia cuando se conocen la potencia y el exponente. Los elementos o partes de la radicación son:


En el último ejemplo se debería buscar un número elevado "a la cuatro" que dé como resultado -81, ¿existirá algún número que cumpla esa condición?
Los ejemplos anteriores se pueden generalizar en el siguiente cuadro:



Video:
Si no entendiste el tema, observa el siguiente video sobre propiedades de los radicales:
3.2. RADICALES CON ÍNDICE DIFERENTE Y BASE IGUAL
Si a € R y m, n € Z+, entonces se cumple que:

Video:
Si no entendiste el tema, observa el siguiente video:
o también puedes repasar en esta página: https://www.superprof.es/apuntes/escolar/matematicas/aritmetica/reales/suma-de-radicales.html





4.1. Para simplificar radicales es preciso tener en cuenta que:
a. El radicando debe ser un producto. Por eso es necesario factorizarlo y descomponer las
constantes o coeficientes numéricos en factores primos.
b. Si el exponente de algún factor es mayor que el índice del radical, este se descompone en
dos factores, de tal manera que el exponente de uno de ellos sea divisible por el índice y el
exponente del otro factor sea menor que el índice.
c. Aplicar las propiedades de los radicales para simplificar cada factor.
4.2. Un radical esta simplificado cuando:
a. El radicando no contiene factores de potencia mayor o igual al índice del radical.
b. La potencia del radicando y el índice radical no tienen factor común diferente que 1.
c. La expresión dada no debe contener radical en el denominador.
d. La expresión dada no debe contener factores dentro del radical.
Para introducir una cantidad bajo un signo radical se eleva dicha cantidad a la potencia que
indique el índice del radical.

4.3. Reducir a índice común dos o más radicales
Es encontrar radicales equivalentes a los dados que tengan el mismo índice.
Un índice común es cualquier múltiplo del m.c.m. de los índices.
El mínimo índice común es el m.c.m. de los índices, habitualmente se elige éste.
Ejemplo1:
Reducir a índice común los siguientes radicales:

b. Dividimos el común índice (12) por cada uno de los índices (2, 3 y 4) y cada resultado obtenido se multiplica por sus exponentes correspondientes.

Ejemplo2:
Reducir a índice común los siguientes radicales:


Ejemplo3:
Reducir a índice común:


Actividad5:



5. OPERACIONES CON RADICALES

5.1. ADICIÓN Y SUSTRACCIÓN
Radicales semejantes
Radicales semejantes son aquellos que tienen el mismo índice y el mismo radicando. Pueden diferir únicamente en el coeficiente que los multiplica.
Para comprobar si dos radicales son semejantes o no, se simplifican, si se puede y se extraen todos los factores que sea posible.
Ejemplo:
Comprobar si los radicales que aparecen en la imagen son semejantes:

SI SON SEMEJANTES PORQUE TIENE EL MISMO ÍNDICE Y EL MISMO RADICANDO.
Procedimiento para sumar o restar radicales
Para sumar o restar radicales se necesita que sean semejantes (que tengan el mismo índice y el mismo radicando), cuando esto ocurre se suman o restan los coeficientes de fuera y se deja el mismo radical. Se escribe a continuación los no semejantes.
Ejemplo1:

Ejemplo2:

Ejemplo3:

Ejemplo4:

Videos:
Antes de continuar, te invito a observar los siguientes videos sobre suma y resta de radicales:
Actividad6:
Nota: TODAS LAS RESPUESTAS DE LOS EJERCICIOS DEBEN JUSTIFICARSE CON LAS RESPECTIVAS OPERACIONES, PROCEDIMIENTOS O PROCESOS EN EL CUADERNO.
1. Resuelve las operaciones (Debajo de la tabla) y Coloca en la esquina superior izquierda de cada cuadro el resulta correcto que corresponda:

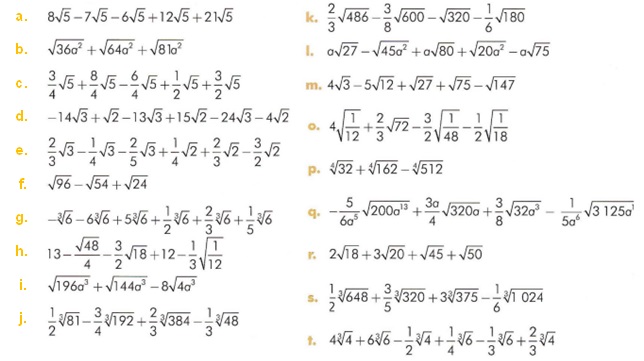

5.2. MULTIPLICACIÓN Y DIVISIÓN
Para multiplicar radicales es necesario distinguir dos casos:
1. Cuando los radicales tienen el mismo índice, se multiplican los radicandos y se deja el mismo índice

Dividimos el común múltiplo (12) por cada uno de los índices (2,3,4) y
cada resultado obtenido se multiplica por sus exponentes correspondientes
(1,2,3). Realizamos el producto de potencias con la misma base en el radicando
y extraemos factores del radicando


Como los dos radicales tienen el mismo índice lo ponemos todo en un radical con el mismo índice. Descomponemos en factores, hacemos la división de potencias con la misma base Simplificamos el radical dividiendo el índice y el exponente del radicando por 3
2. Cuando los radicales tienen distinto índice, primero se reducen a común índice y luego se dividen.
Ejemplo1:

En primer reducimos a común índice por lo que tenemos que calcular el mínimo común múltiplo de los índices, que será el común índice. m.c.m(3,2) = 6
Dividimos el común índice (6) por cada uno de los índices (3 y 2) y cada resultado obtenido se
multiplica por sus exponentes correspondientes (1 y 1)
Descomponemos el 4 en factores para poder hacer la división de potencias con la misma base y dividimos




Videos:
Antes de continuar observa los siguientes videos:
multiplicación y división de radicales de diferente índice:
Radicales del mismo índice:
Actividad7:
NOTA: TODAS LAS RESPUESTAS DE LOS EJERCICIOS DEBEN JUSTIFICARSE CON LAS RESPECTIVAS OPERACIONES, PROCEDIMIENTOS O PROCESOS.
1. Resuelve las siguientes multiplicaciones:





6· RACIONALIZACIÓN
La racionalización de radicales consiste en quitar los radicales del denominador, lo que permite facilitar el cálculo de operaciones como la suma de fracciones.
Podemos distinguir tres casos:
Caso
1: Racionalización del tipo:




Y en general cuando el denominador sea un binomio con al menos un radical.
Se multiplica el numerador y denominador por el conjugado del denominador.
El conjugado de un binomio es igual al binomio con el signo central cambiado:

También tenemos que tener en cuenta que: "suma por diferencia es
igual a diferencia de cuadrados".

Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados

Multiplicamos numerador y denominador por el conjugado del denominador, quitamos paréntesis en el numerador y efectuamos la suma por diferencia en el denominador, por lo que obtenemos una diferencia de cuadrados

Videos:
Si se te dificulta entender el tema, te invito a observar los siguientes videos:
Actividad8:
NOTA: TODAS LAS RESPUESTAS DE LOS EJERCICIOS DEBEN JUSTIFICARSE CON LAS RESPECTIVAS OPERACIONES, PROCEDIMIENTOS O PROCESOS.
1. Racionaliza el denominador de las siguientes expresiones:



HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%): a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%): a. Prueba Bimestral
• Ser - Convivir (25%): a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
